注意这篇中套筒是共源共栅放大器其实是Ldo电路的一部分,但在实际Ldo设计中其由于增益过大会给后续调整Ldo电路带来困难,故这篇文章并不完整;推荐参考此文章的思路设计折叠式设计套筒是共源共栅放大器来作为Ldo电路的Amp
运输放大器设计
1.理论设计
设计一个运输放大器,其性能指标为:
| $CL=5pF$ | $0.5V<V_{out-range}<2.5V$ | $A_V>20000$ |
|---|---|---|
| $V_{DD}=3.3V$ | $GBW =20MHz$ | $Phase margin>60deg$ |
对于$A_V>20000$的要求,我们采用第一级大增益,第二级还行的增益:
- 第一级:Cascode结构要达到10000左右的增益
- 第二级:采用简单P和Nmos的对管结构,增益可以再个位数
这样子很轻松的就可以达到$A_V>20000$
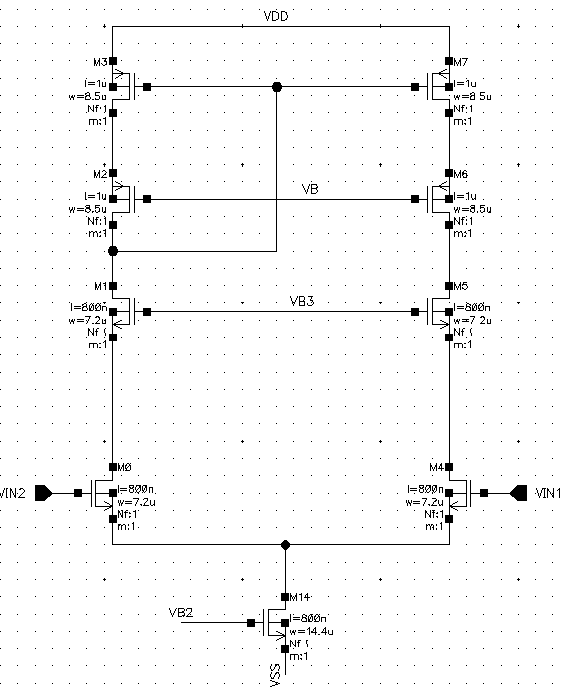
但对于输入$V_{in}$来说,这样的结构天生上限被$V_{B3}$限制$V_{B3}-(V_{gs}-V_{th})$,为:
$$
V_{lim-max}<V_{B3}-V_{gs}+V_{th}
$$
我们要加入偏置电路(下图红框)使M14的漏极与$V_{B3}$的差恒定,让$V_{B3}$能随着$V_{in}$增大而增大
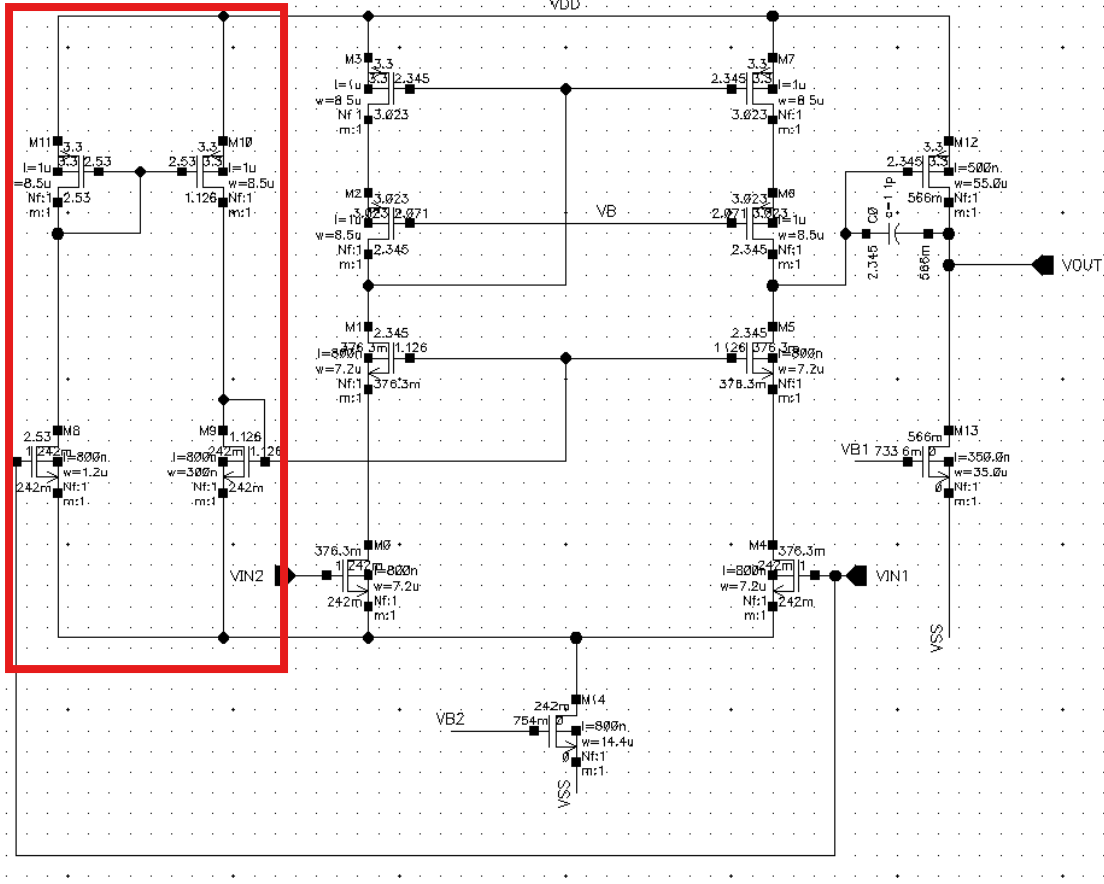
在图中M8管和输入对管M0和M4的W/L,为了使偏置电路上的电流尽可能小,有如下关系:
$$
\frac 16 \cdot (\frac WL){M0}=(\frac WL){M8}
$$
在偏置电路中,我们假设Nmos的$V_{OD}$都相同;M8和M9的电流,由于电流镜电流相同,有:
$$
I_{D9}=I_{D8}
$$
根据$I_D=\frac 12 \mu C_{ox} \frac WL (V_{gs}-V_{th})^2$,且M8和M9栅极不链接在一起,有:
对于M8来说:
$$
V_{g8}=V_{gs11}+V_{B2}=(V_{gs11}-V_{th})+V_{B2}+V_{th}=V_{OD}+V_{th}
$$
对于M9来说:
$$
V_{g9}=V_{gs5}+V_{gs11}-V_{th}+V_{B2}=(V_{gs5}-V_{th})+(V_{gs11}-V_{th})+V_{th}
$$
$$
V_{g9}=2 \cdot V_{OD}+V_{th}
$$
带入饱和区电流方程可以得到:
$$
\frac 12 \mu C_{ox} (\frac WL)8 (V{OD}+V_{th}-V_{th})^2=\frac 12 \mu C_{ox} (\frac WL)9 2 \cdot (V{OD}+V_{th}-V_{th})^2
$$
化简得:
$$
\frac 12 \mu C_{ox} (\frac WL)8 (V{OD})^2=\frac 12 \mu C_{ox} (\frac WL)9 \cdot 4 \cdot V{OD}^2
$$
最终得到:
$$
\frac 14 \cdot (\frac WL){M8}=(\frac WL){M9}
$$
2.参数确定:
继续计算GBW,即增益为0的点:
$$
GBW=P_1 \cdot A_{Vall}=P_1 \cdot A_1 \cdot A_2
$$
在下式分母中$1+A_2 \approx A_2$:
$$
GBW=\frac {A_1 \cdot A_2}{R_{OUT1}(1+A_2)C_C}=\frac {A_1}{R_{OUT1}C_C}=\frac {g_{m1}}{C_C}
$$
主极点$P_2=\frac {g_{m2}}{C_L}$,零点$Z=\frac {g_{m2}}{C_C}$
我们取:
$$
Z > 10GBW \rightarrow g_{m2}=10g_{m1}
$$
要满足$Ph>60deg$:
$$
P_2>2.2GBW \rightarrow C_C=0.22 \cdot C_L=1.1pF
$$
$$
g_{m1}=GBW \cdot C_C=20M \cdot 2 \pi \cdot 1.1pF \approx 136u
$$
在前面我们确定$g_m$有如下关系:
$g_{m2}=10g_{m1}$
故:
$$
g_{m2}=10g_{m1}=1360u
$$
接下来用gmid设计法则确定各支路的电流,取gm/id=16有:
$$
I_{D-M0,M4}=\frac {136u}{12} \approx 8.5uA
$$
$$
I_{D-M12}=\frac {1360u}{16} \approx 85uA
$$
为了使次极点在GBW外,实际我们取$g_{m2}=1500u$,故实际电流可以得到:
$$
I_{D-M12}=\frac {1500u}{16} \approx 93uA
$$
知道了各支路的电流,可以求尾电流源的电流大小:
由$I_D=\frac 12 \mu C_{ox} \frac WL (V_{gs}-V_{th})^2$可得到:
$$
\frac {I_{D8}}{I_{D0}}=\frac {(\frac WL){M8}}{ (\frac WL){M0}}=6
$$
故偏置电路上的电流为:
$$
I_{D-M8}=\frac {8.5uA}{6} \approx 1.4uA
$$
观察电流可以看到有两条偏置电路上的电流$I_{D-M8}$,两条Cascdoe电流$I_{D-M0,M4}$流过尾电流源:
$$
I_{ss}=2 \cdot 8.5uA + 2 \cdot 1.4uA =19.8uA
$$
3.电路设计参数表
至此我们可以给出各个电路的设计参数:
| $g_{m1}$ | $136uA$ |
|---|---|
| $g_{m2}$ | $1360uA$ |
| $I_{D-M0,M4}$ | $8.5uA$ |
| $I_{D-M12}$ | $85uA$实际是$93uA$ |
| $I_{D-M8}$ | $1.4uA$ |
| $I_{ss}$ | 19.8uA |
4.Nmos设计
4.1输入四管Nmos
我们取最小L=800n,gmid前文提到我们设置成16
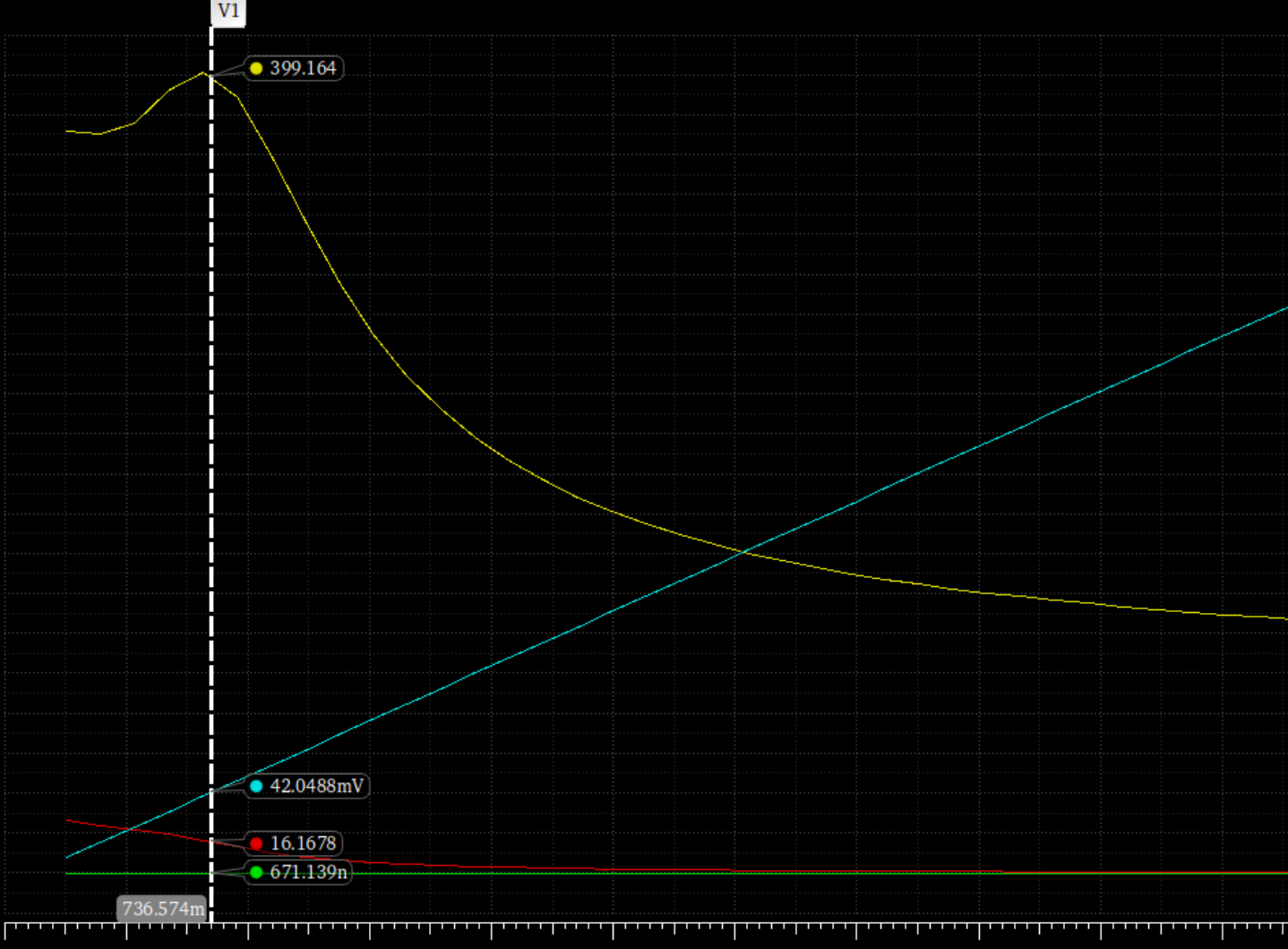
根据仿真结果,1W对应电流为671n,我们总共需要$8.5uA$的电流:
$$
\frac {8.5uA}{671n}=12.4u
$$
故输入的四个Nmos我们取:
$$
\frac WL=\frac {12.4u}{800n}
$$
4.2负载管ss
gmid取15,降低噪声,L取大一点,L=1u
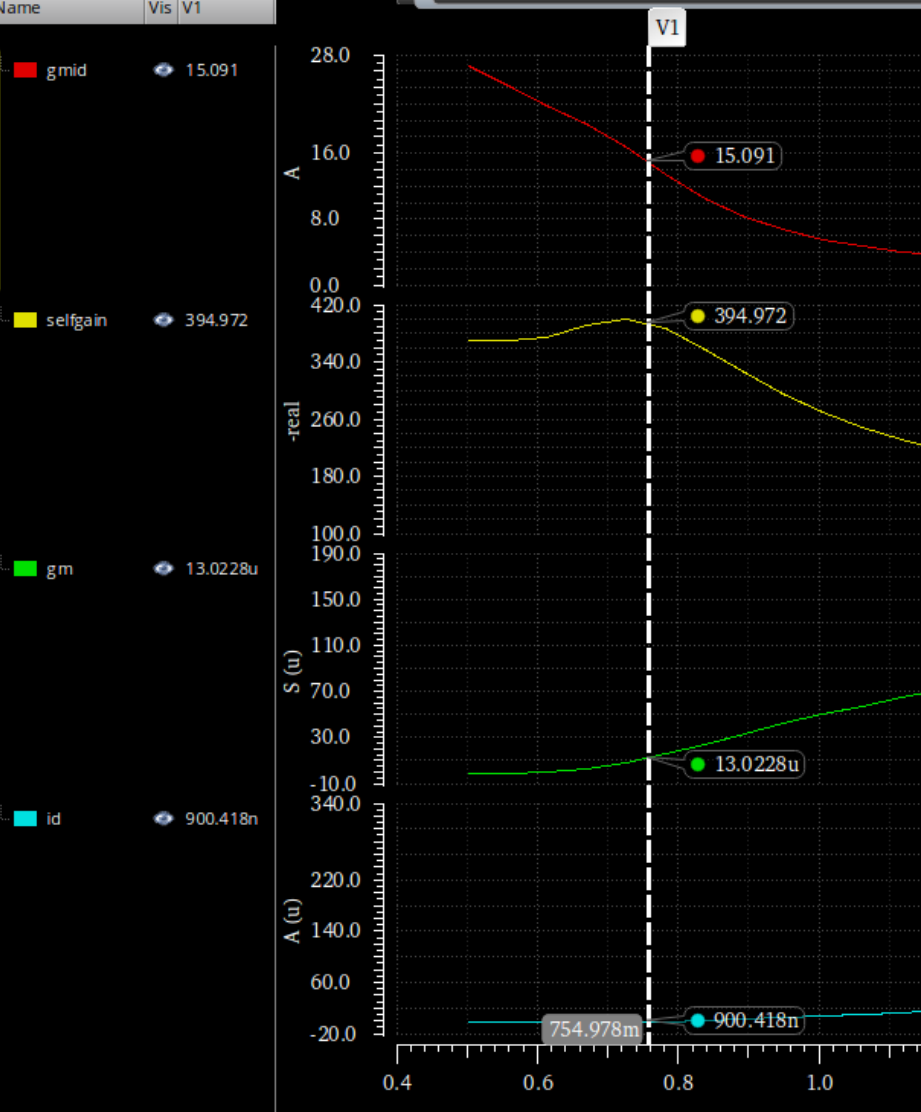
输出对管的Nmos,gmid取小一点取12
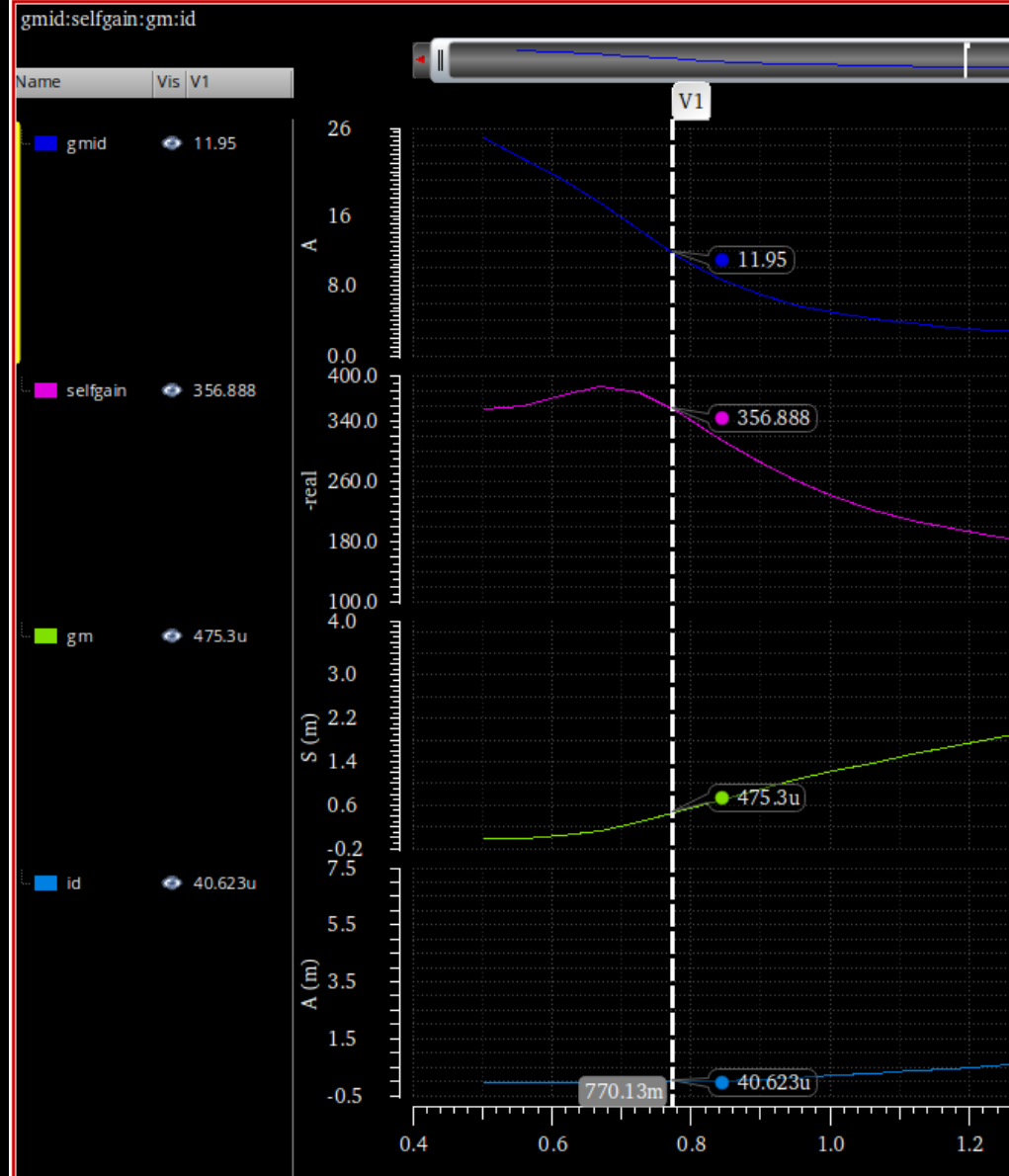
22u/800n 22u/400n
5.Pmos设计
设计cascode上面四个Pmos以及两个偏置电路中的Pmos,它们都是负载管我们尽量把其L取大,取L=1u,要让它的$Vov\approx200mV$
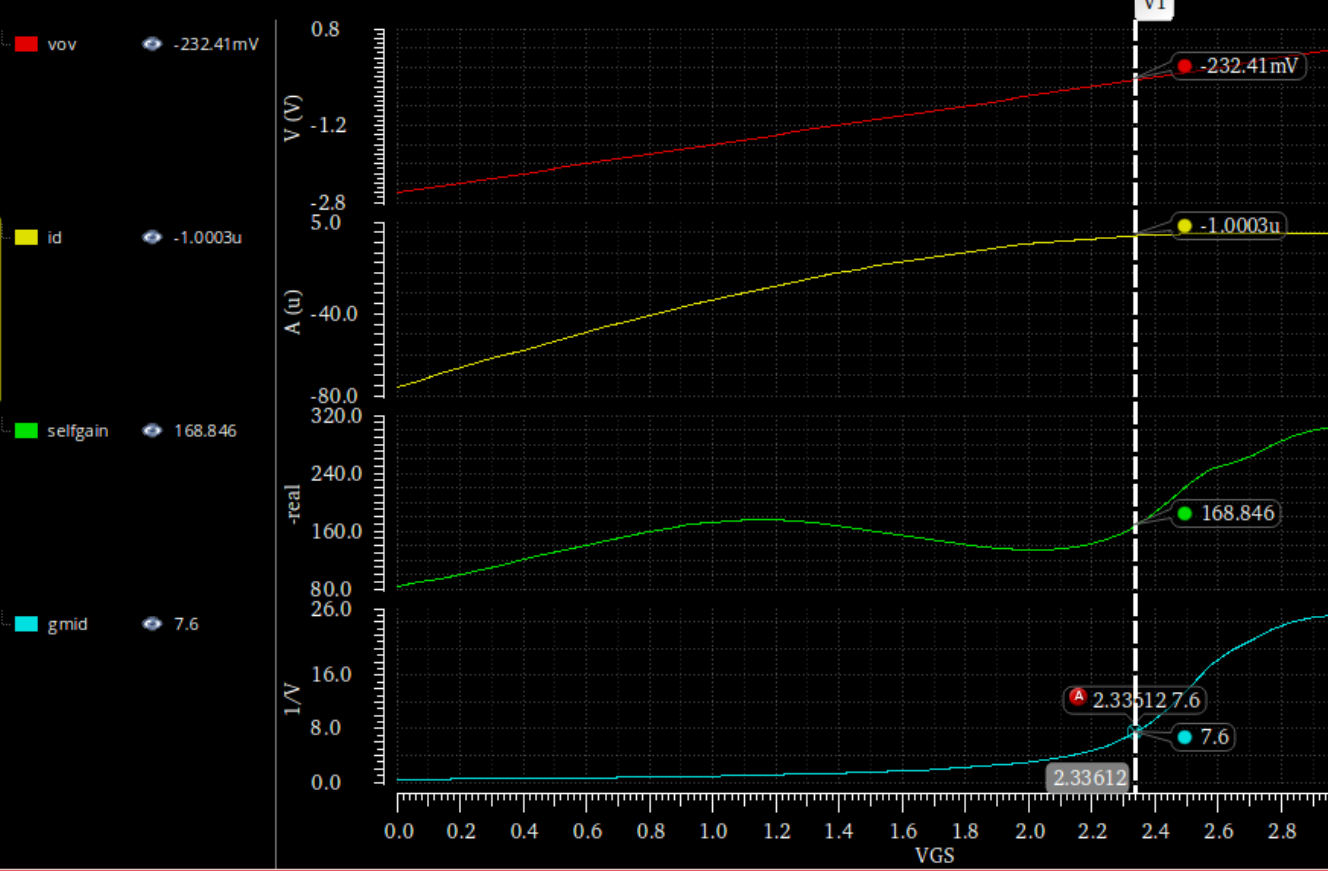
由上图取gmid=7.6,差不多满足Vov在200mV的要求,此时$I_d=1u$
$$
W=\frac {8.5u}{1u}=8.5u
$$
输出管Pmos的Vov与上面几个Pmos的相同:其Vov=232mV,gm=1.5m,保持,其$I_d=93uA$,W差不多要扩大十倍,可以缩小二倍L,扩大五倍W
$$
\frac WL=8.5=\frac {44.2u}{340n}
$$
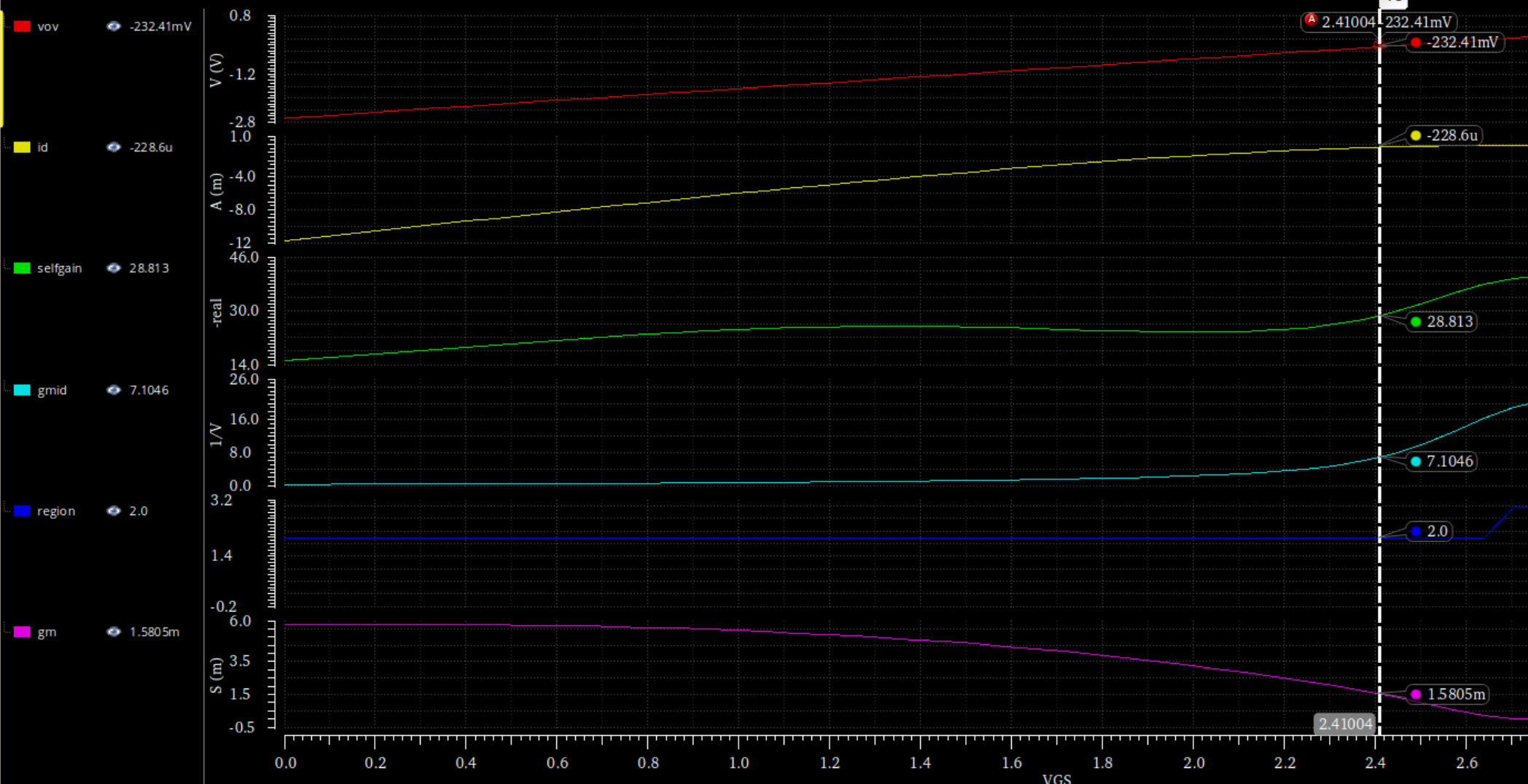
发现基本符合,可以选择,且VB1的电流源电流应该跟上图的id相同为228.6uA
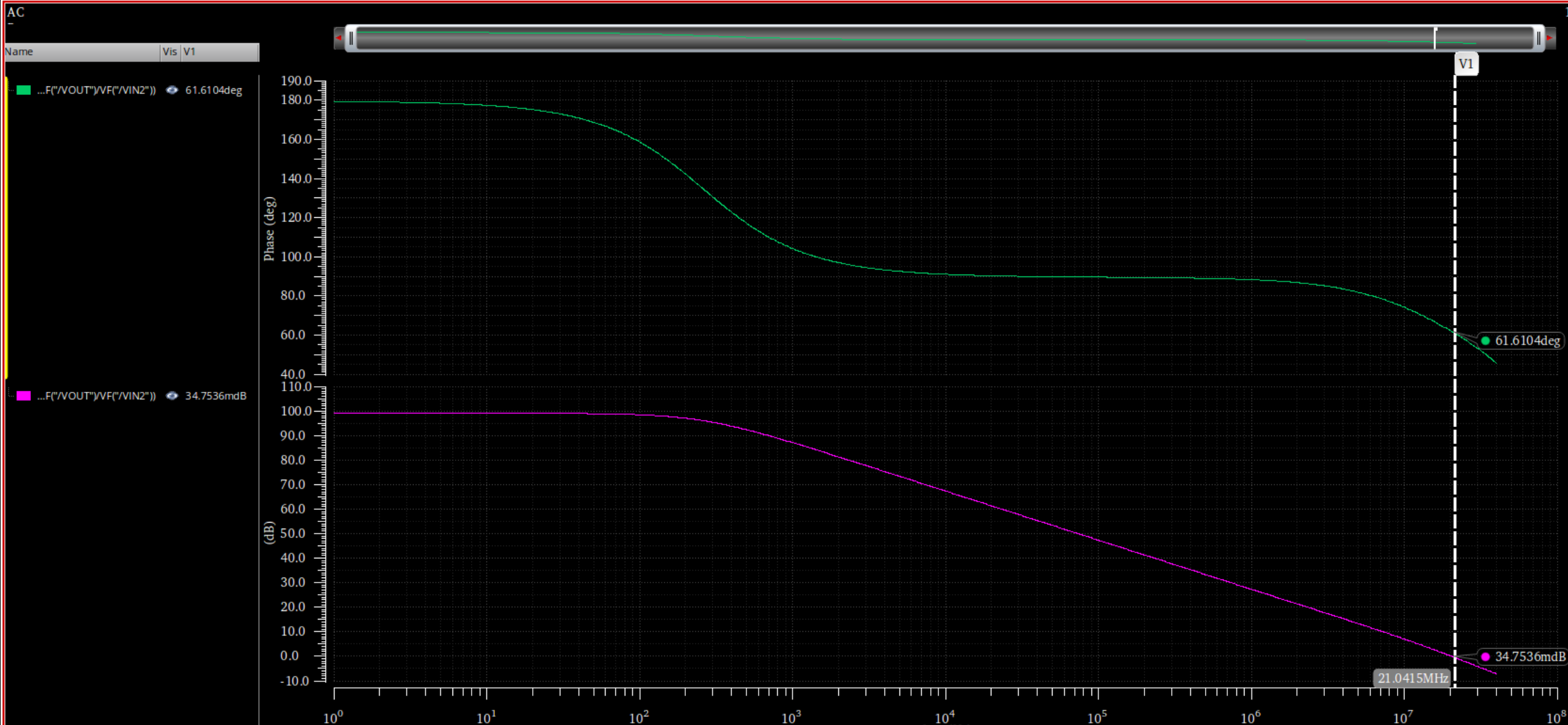
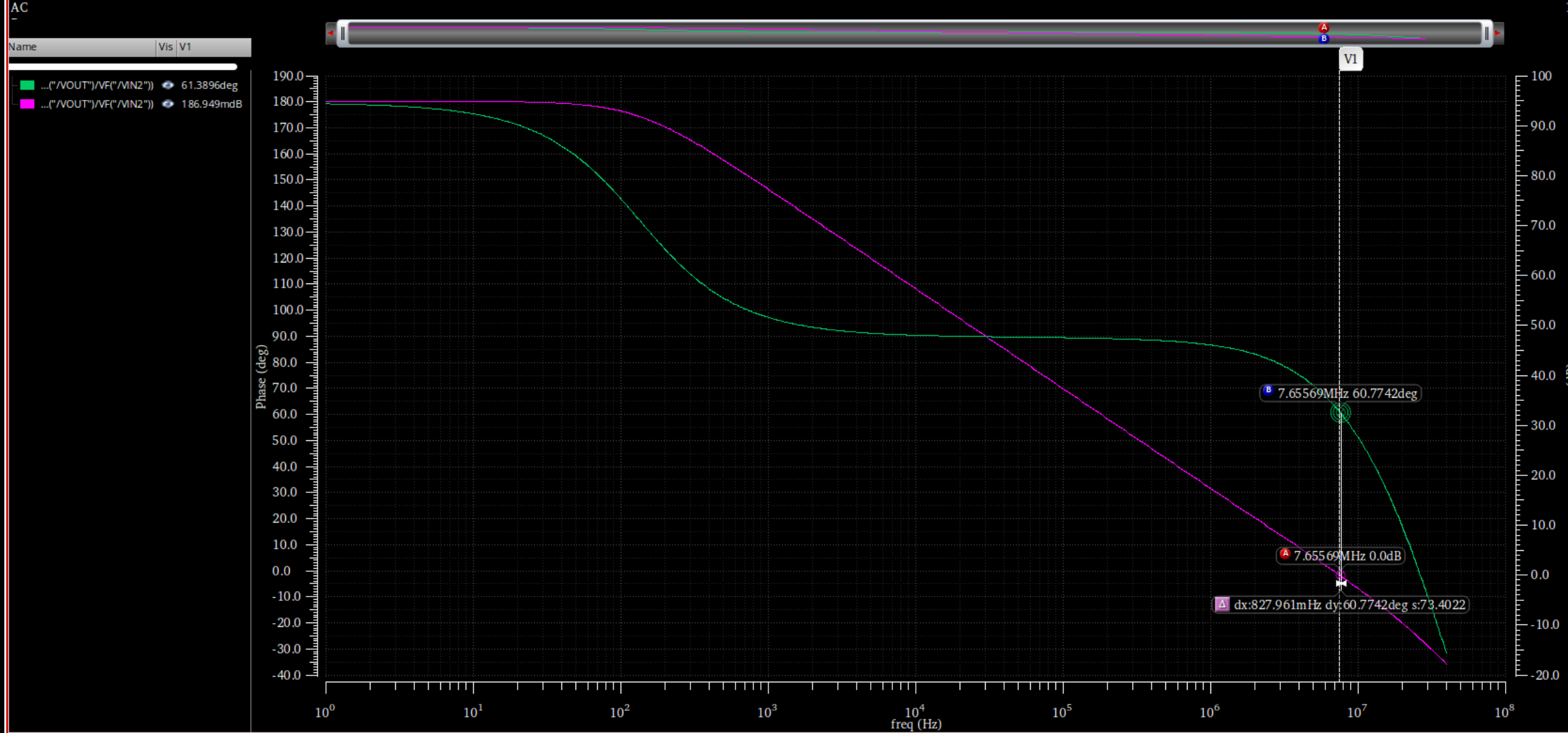
AC仿真
两级运放0dB时勉强达到60deg,满足ph>60deg,此时输出支路的id被推的非常高来让gm=1.34m,$C_C=3.5pF$
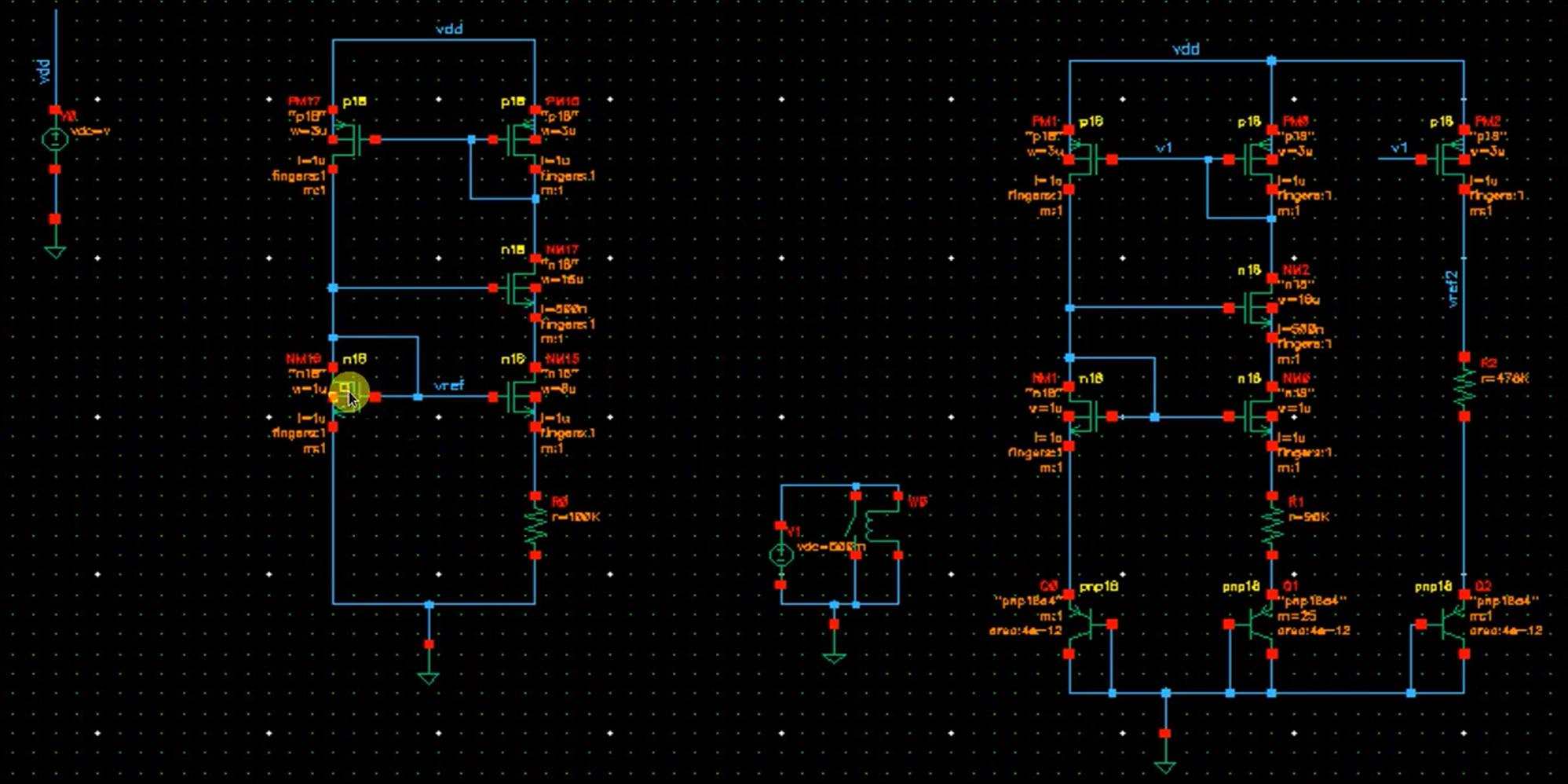
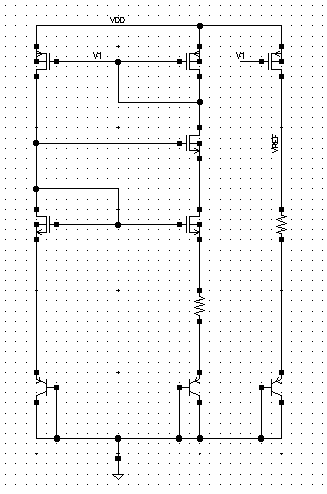
偏置网络的设计
我们希望得到一个与$V_{DD}$和温度变化无关的电压,用电路的自身关系,我们设置一个电阻和一个二极管接法的mos,他们的电流相同,从上端看入的电压也相同,在绘制他们的IV特性的直线和曲线会相交于一点$V_{2}$,把稳定电压在$V_{2}$
但是这种接法的电流,mos管的电流会分到电阻上,要引入隔离管,让mos管维持饱和,负反馈可以稳定输出,且隔离管的g到s没有通路,也解决了上面mos分流的问题
1.与电源VDD无关的电源
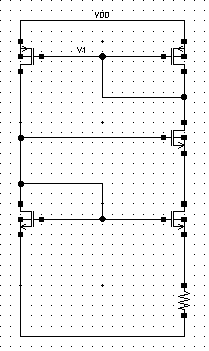
图上的是电源抑制网络,实现了与电源VDD无关的电压,在设计时我们我要让左边的管子M1的$V_{gs}$小于右边的管子M2,他们的宽长比如下关系:
$$
(\frac WL){M1}<(\frac WL){M2}
$$
由因为:
$$
V_{gs1}<V_{gs2}
$$
多出来的$\Delta V_{gs}=V_{gs2}-V_{gs1}$将被电阻R分得,有:
$$
I_R =\frac {\Delta V_{gs}}{R}
$$
2.与温度无关的电源
要综合
- PTAT温度正系数电路
- CTAT温度负系数电路
2.1PTAT温度正系数电路
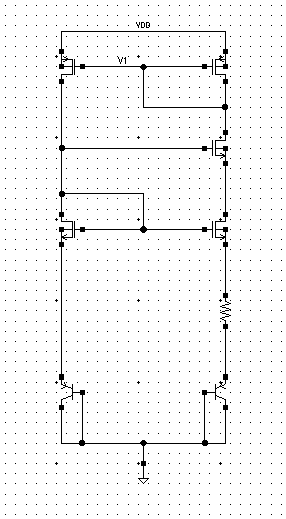
$$
\Delta V_{BE}=\frac {KT}{q}ln \frac {A_2}{A_1}
$$
其与温度是正相关的
2.2CTAT温度负系数电路
二极管两端电压随着温度升高而减小(非线性关系)
2.3不受温度影响电路
在仿真中VREF到BJT下端应该是一个抛物线
LDO电路设计:
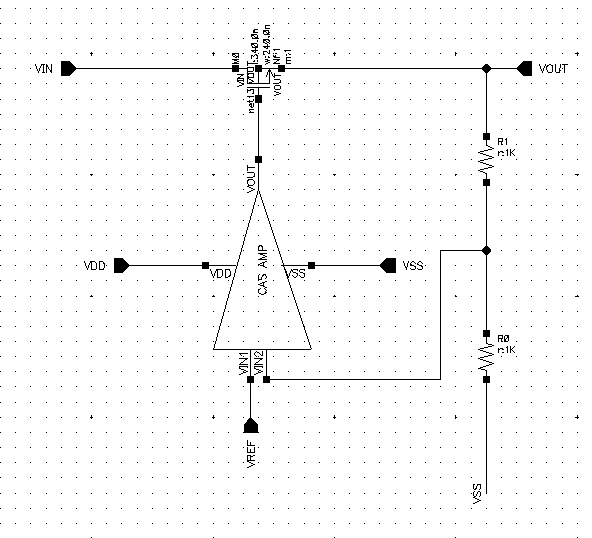
VREF处将接一个Bandgap电压源作参考电压,假设我们输入一个2.2V的不规整信号,希望输出一个1.8V的稳定电压;由如下公式:
$$
V_{OUT}=(1+\frac {R_1}{R_0}) \cdot V_{IN}
$$
可以解出:
$$
\frac {R_1}{R_0}=\frac 12
$$
电路参数验证:
发现GBW对应的61deg