在virtuoso中我们搭建出如下的一个电路:
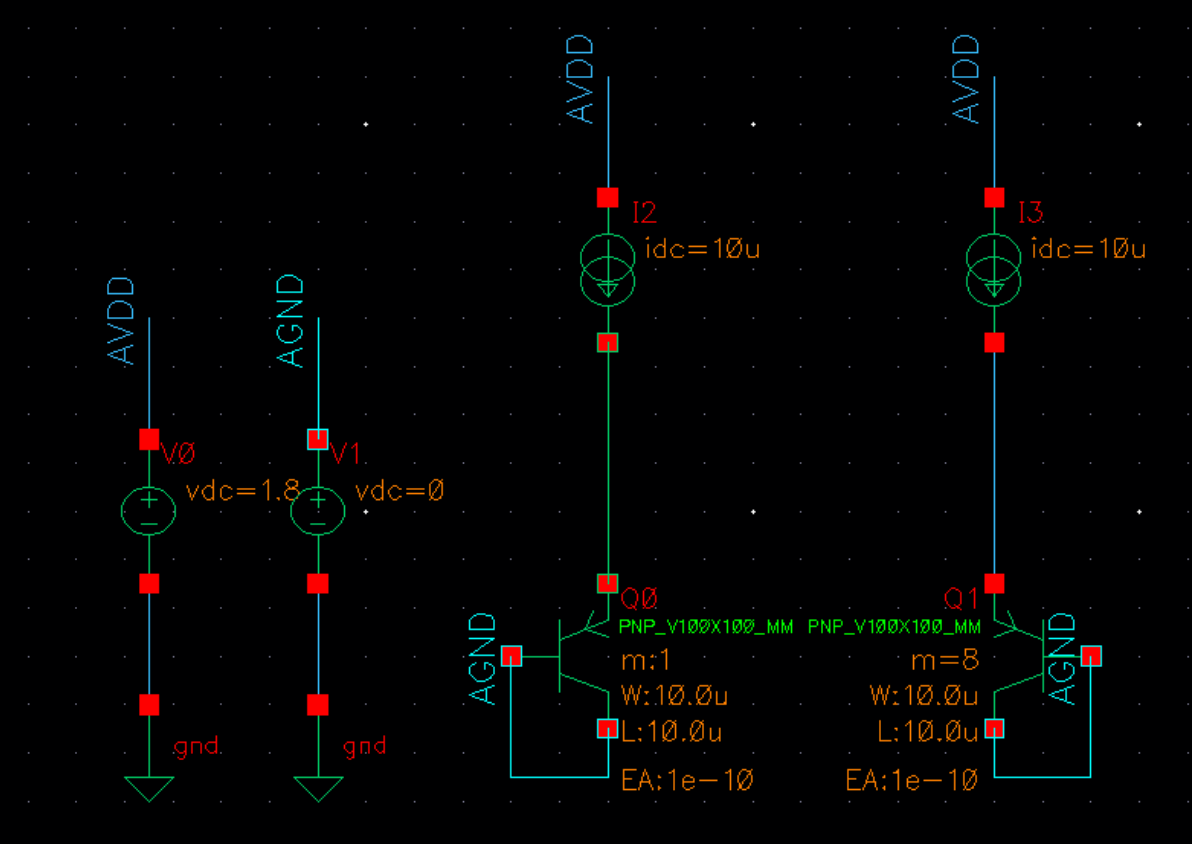
注意右边的PNP BJT的multipler要改为8,再点击ADE L创建一个从-40度到125度的dc仿真,点击仿真完成后,选择Results-Direct Plot-Main Form
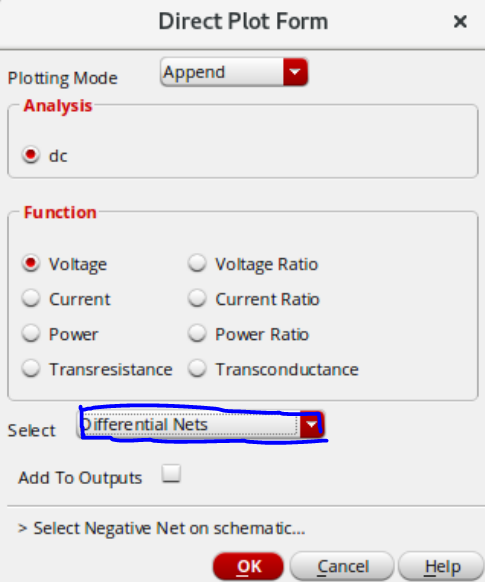
在上图的中蓝框中设定为Differential Nets,然后回到仿真图中先点击1后点击2
可以得到一条斜率负,代表温度系数的直线
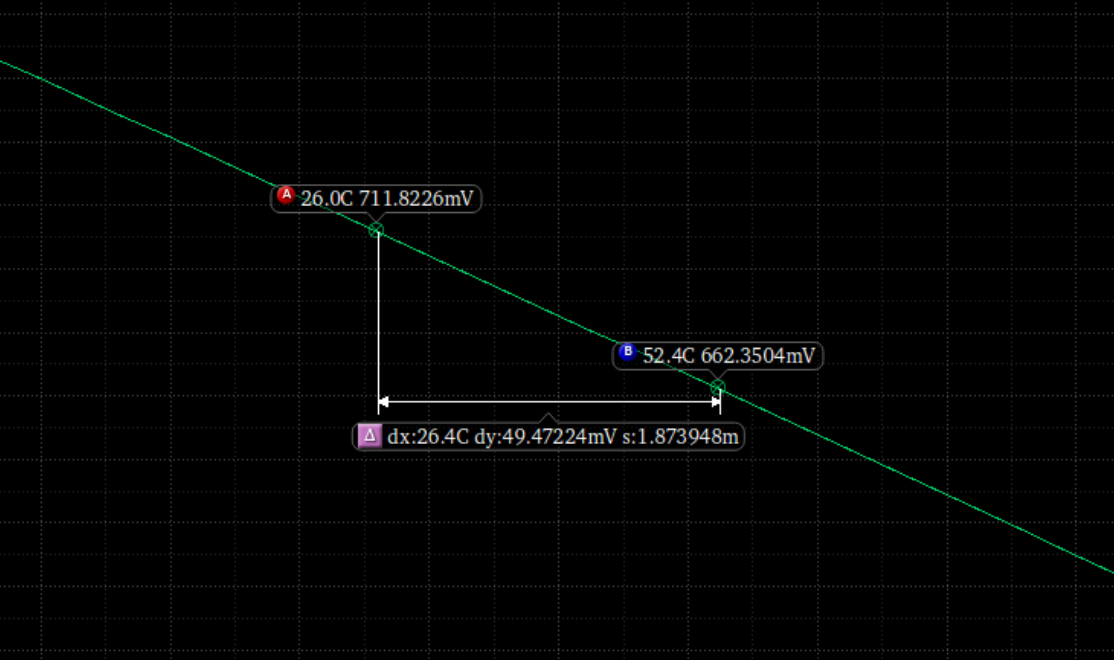
斜率k=1.873m,将代表直线方程送Calculator,得到:(v("/net4" ?result "dc") - v("/AGND" ?result "dc"))
同理按上面的操作再生产右边BJT的负温度曲线
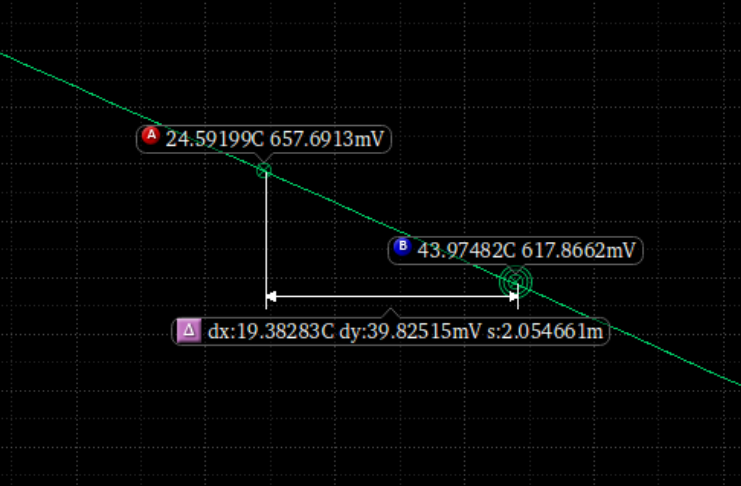
斜率k=1.873m,同样的将代表直线方程送Calculator,得到:v("/net3" ?result "dc") - v("/AGND" ?result "dc"))
在Calculator中将上面两个代表负温度系数的方程相减((第一根直线减去第二根)可以得到正温度系数的直线方程:
1 | (v("/net4" ?result "dc") - v("/AGND" ?result "dc"))-(v("/net3" ?result "dc") - v("/AGND" ?result "dc")) |
其所代表的斜率如图:
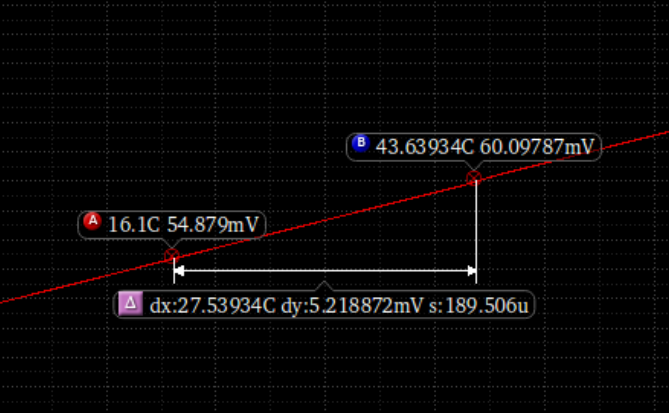
斜率k=189.5u=0.1895m;也就是说,我们要将这个正温度系数的直线斜率扩大m倍到k=1.873m才能让正温度和负温度系数相抵消,得到不受温度影响的电压,由:
$$
m=\frac {1.873m}{0.1895m} \approx 9.88
$$
我们先将正温度系数扩大9.88倍
1 | ((v("/net4" ?result "dc") - v("/AGND" ?result "dc"))-(v("/net3" ?result "dc") - v("/AGND" ?result "dc")))*9.88 |
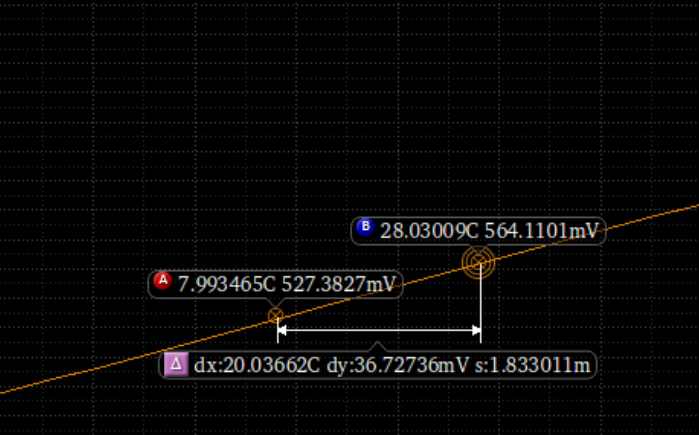
再与下面第一条直线相加:
(v("/net4" ?result "dc") - v("/AGND" ?result "dc"))
可以得到:
1 | ((v("/net4" ?result "dc") - v("/AGND" ?result "dc"))-(v("/net3" ?result "dc") - v("/AGND" ?result "dc")))*9.88+(v("/net4" ?result "dc") - v("/AGND" ?result "dc")) |
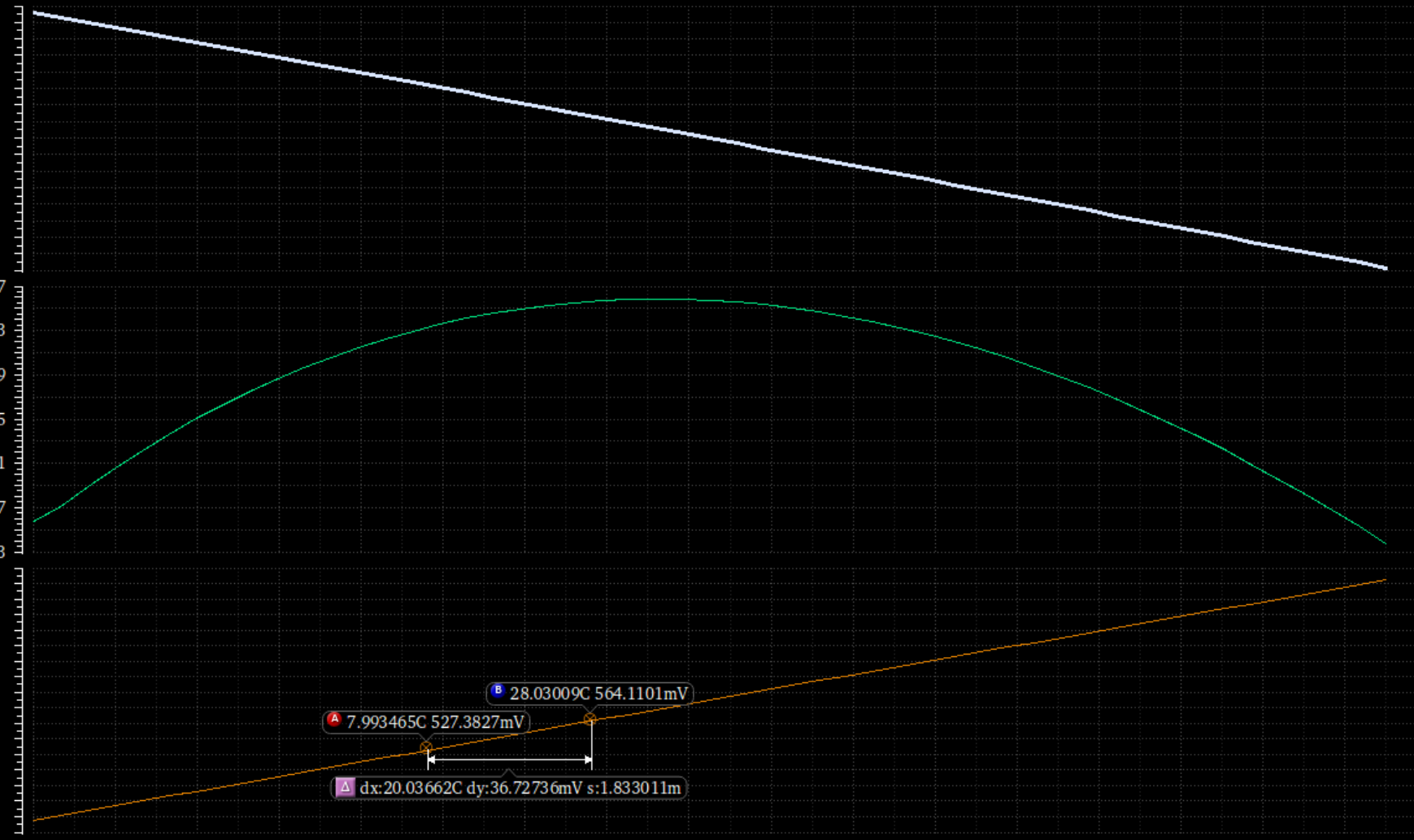
可以看到不受温度影响的电压在大的坐标轴中表现为抛物线
实际偏置电路的设计:
在如下的偏置电路中,我们将所有N和Pmos的L都设置为1u来避免沟道调制效应,在图中两个电阻$R_0,R_1$的比值对应着上文中的m,代表将正温度系数的直线斜率扩大m倍:
$$
m = \frac {R_0}{R_1}
$$
先测量负温度系数直线:依次选择左边PNP的上和下两端
得到以下直线图像
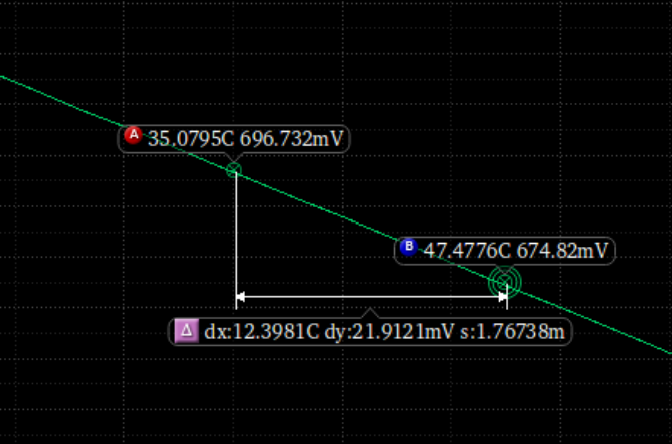
斜率k=1.767m
再测量正温度系数:选择电阻$R_1$的上下两端
得到以下直线
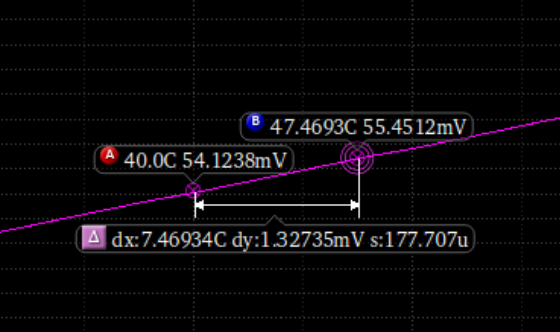
斜率为k=177.7u=0.1777m,用负温度系数除正温度系数:
$$
m=\frac {1.767m}{0.1777m}=9.943
$$
所以$R_1$要扩大:
$$
R_1 = mR_0=5K \cdot 9.943=49.715K
$$
测量正温度和负温度相加,依次点击图红框的上下两端
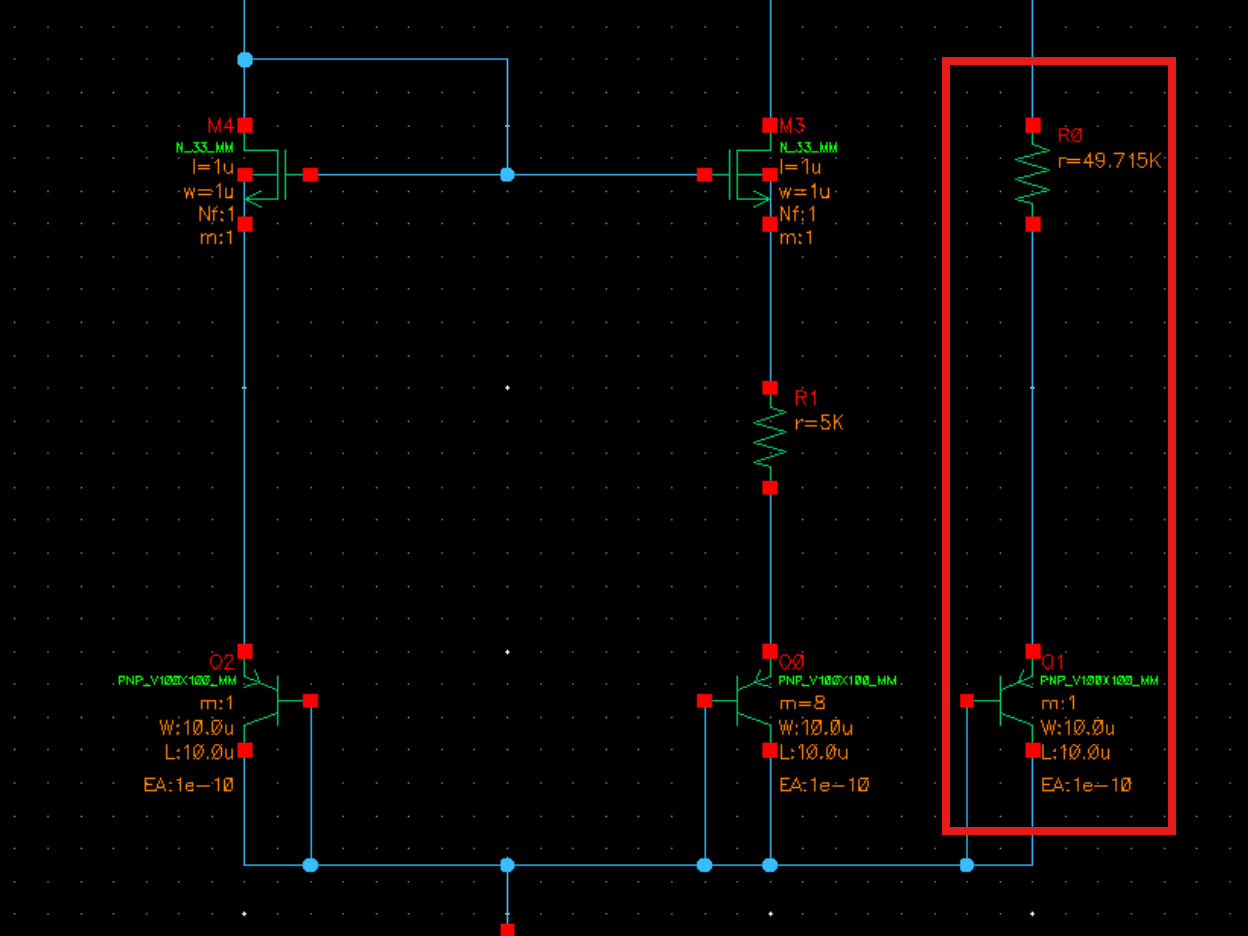
发现得不到一条抛物线,判断管子尺寸有问题,将上下5个mos的改为如下图:
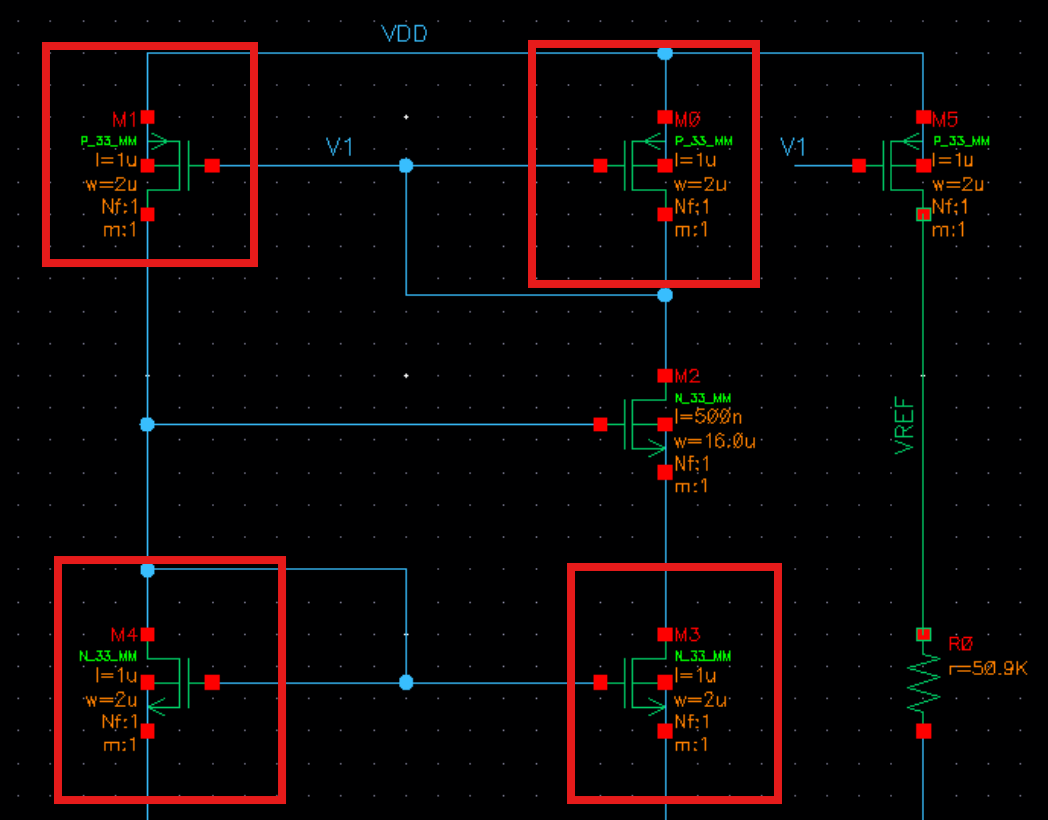
重新测正负温度系数:
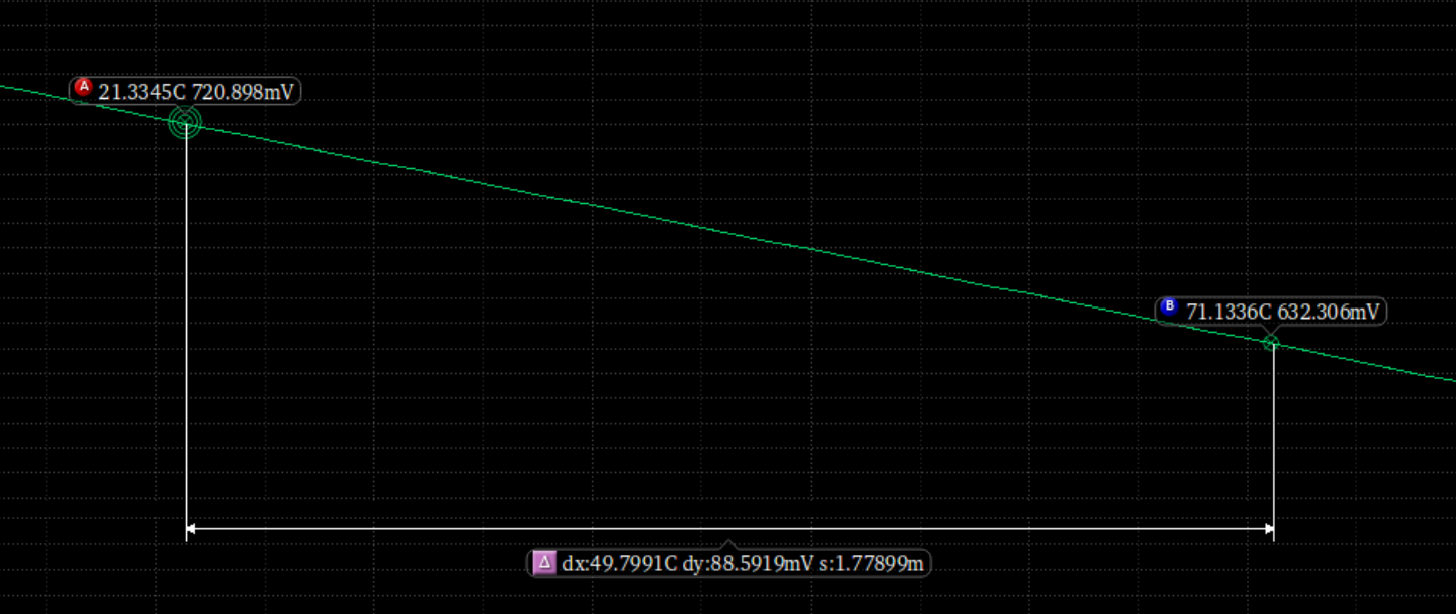
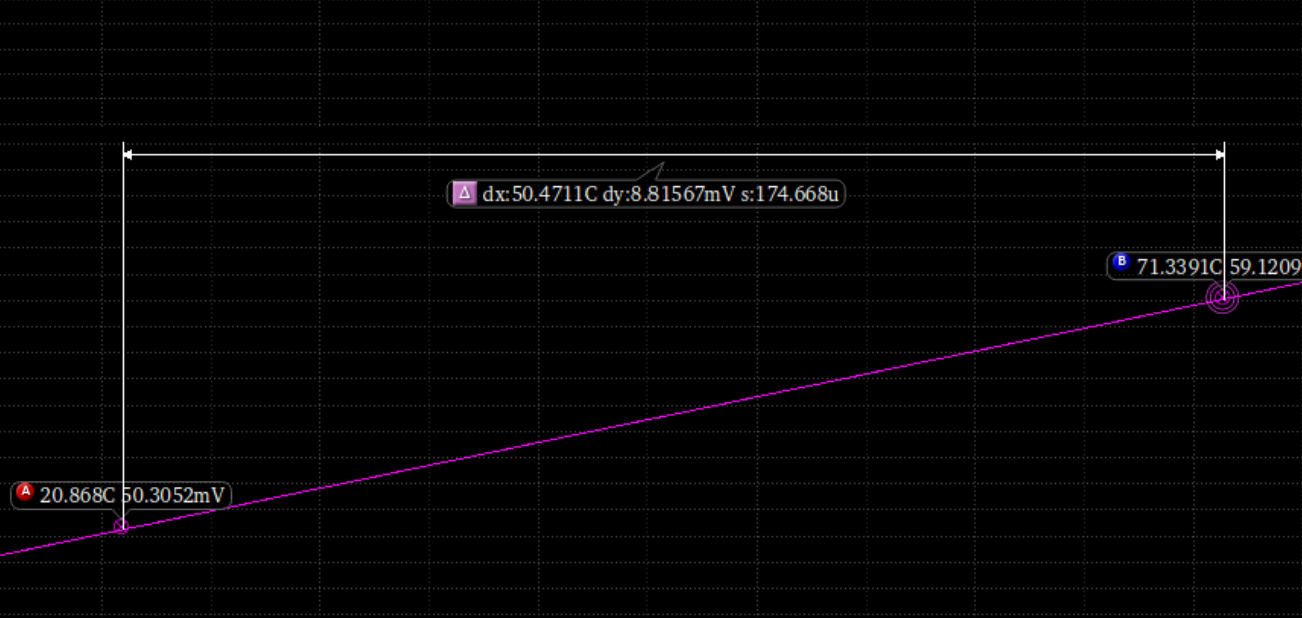
重新计算:
$$
m=\frac {1.77899m}{0.174668m}=10.18497950397325
$$
得到$R_0=50.92489751986626K \approx 50.924K$
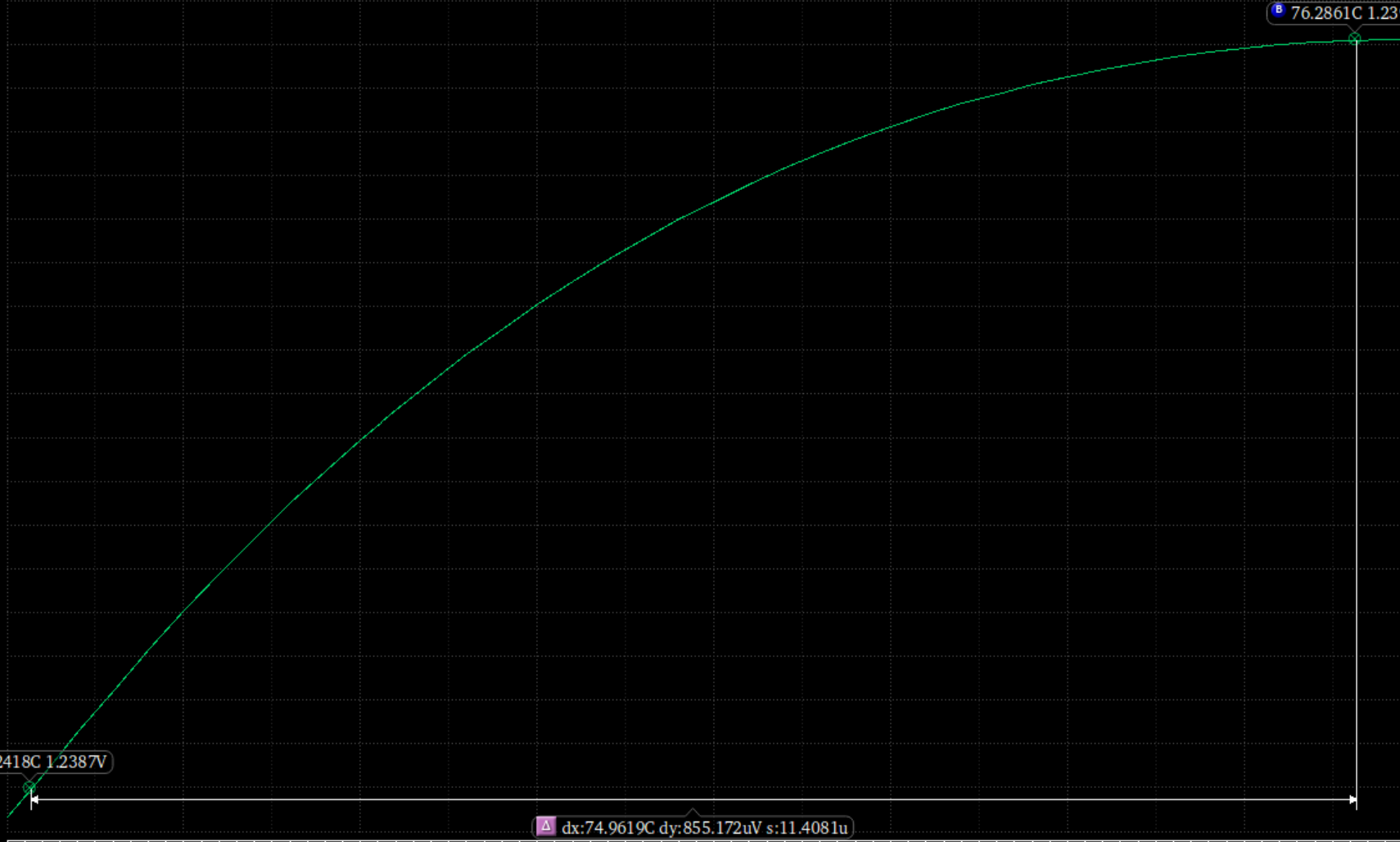
LDO中的偏置电路设计
我们从下面的电源抑制比好的V2这处引出电压
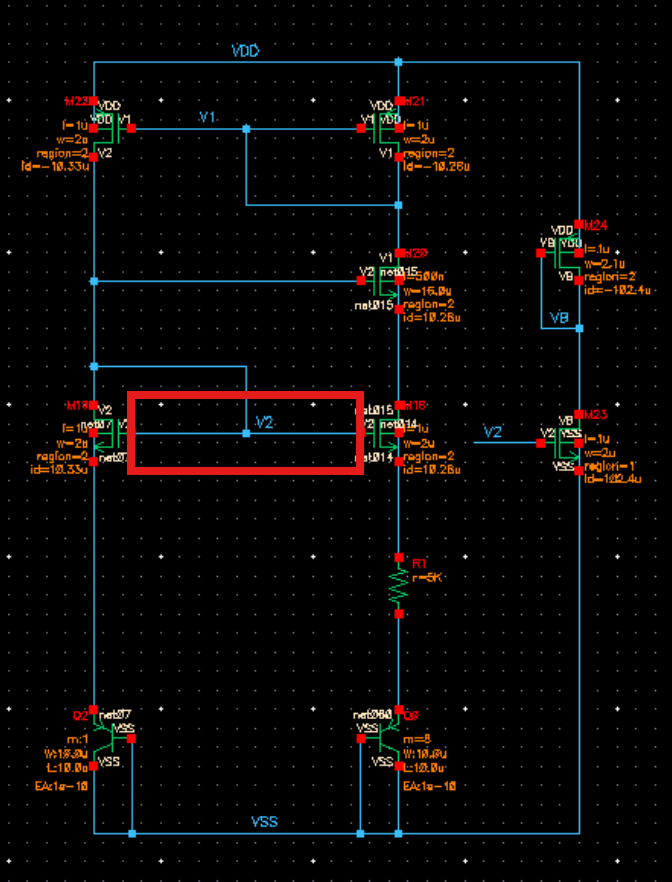
然后进行dc仿真,发现这条支路的电流与实际我们用理想电流源做出的idc=8.5u差距过大
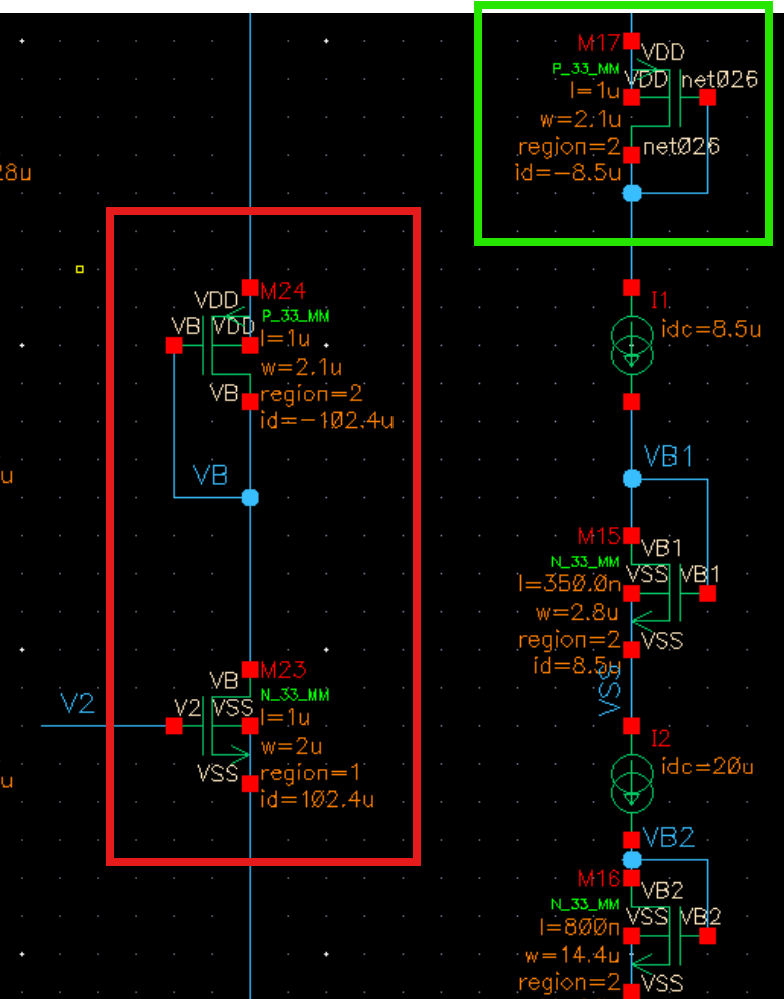
要将红框中的Nmos的L尺寸放大m倍:
$$
m = \frac {102.4u}{8.5u} \approx 12
$$
但在实际中我们不希望偏置的电流过大,希望在1uA左右,在V2处的电压还是过高,我们将V2换到下图中位置
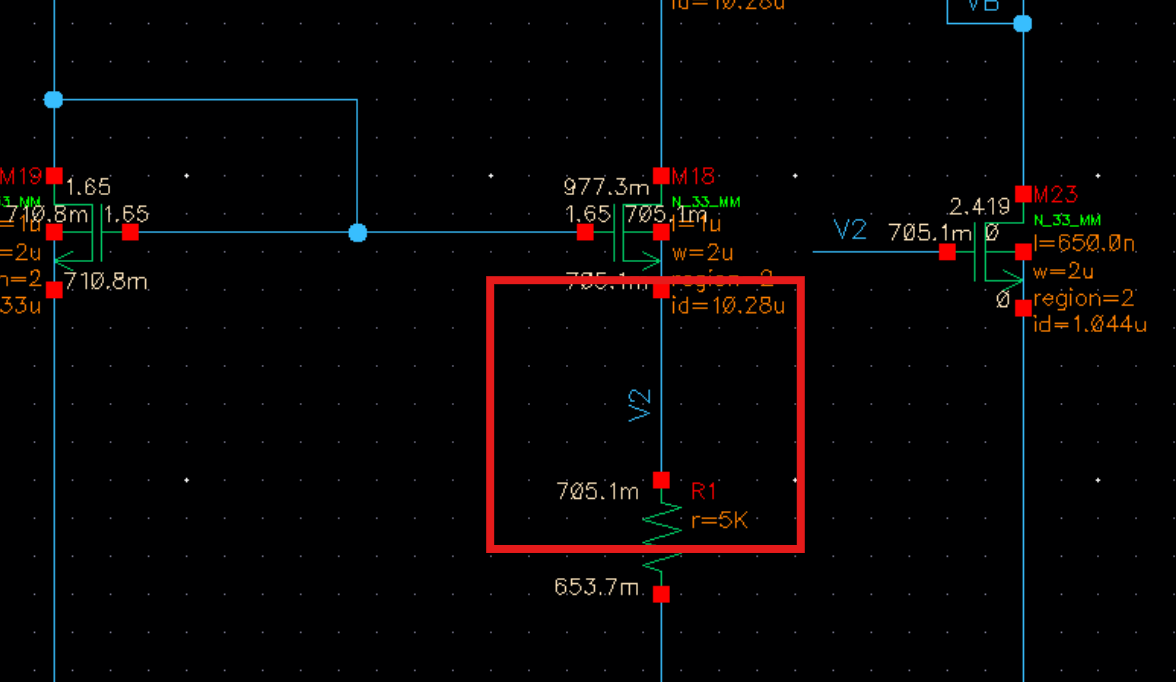
调整M23的L使其Id=1uA,同时因为id变小了,我们希望Vod不变,电流要从8.5uA缩小到1.044uA,L要放大k倍:
$$
k=\frac {8.5u}{1.044u}=8.141
$$
将M24的L扩大8倍,同时再微调L使Vod与原理想电流源的M17的Vod相同
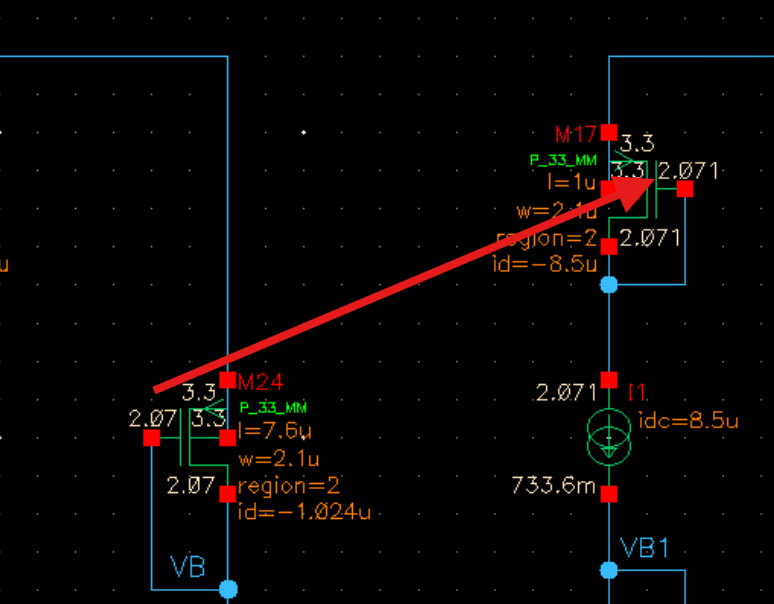
之后所有需要提供偏置电压的地方都按此方法将三端电压与理想电流源出来的电压相等