前言——为什么需要gmid设计法
1.为什么需要
为什么需要$\frac {g_m}{i_d}$,其与L和工艺无关其本质是:用功耗换增益可以理解为用多少电流换取多少$g_m$,通过的电流越大换取的$g_m$越大,带来的增益就越高,通常来说$i_d$在$\mu A$数量级
其次还要考虑$f_t$管子的速度,代表能处理多高频率的信号,随着工艺的进步,管子将越来越像开关,这里给出简要表达式:
$$
f_t=\frac 1{2\pi} \cdot \frac {g_m}{C_{gs}}
$$
其中:
- $g_m$为管子的跨导
- $C_{gs}$为栅极的寄生电容
2.主要设计流程:
- 选定要先选定过驱动电压$V_{OV}=V_{GS}-V_{TH}$,确定直流工作点,其与增益密切相关,在Cadence中为
waveVsWave(?x gmid ?y id) - 再选定管子的尺寸L,其会直接影响管子的输出抗抗,与本征增益和频率特征相关
- 最后再 来对不同类型的管子定$\frac {g_m}{i_d}$
- 放大管:需要高增益,其$g_m$要大一点,$\frac {g_m}{i_d}$的值偏大
- 电流镜:需要降低噪声,$\frac {g_m}{i_d}$要尽量小
理论——对$Nmos$扫参仿真得到参数以及基本操作
先搭建如图的原理图:把漏端和栅端连接在一起,从而忽略$V_{ds}$对管子性能的影响
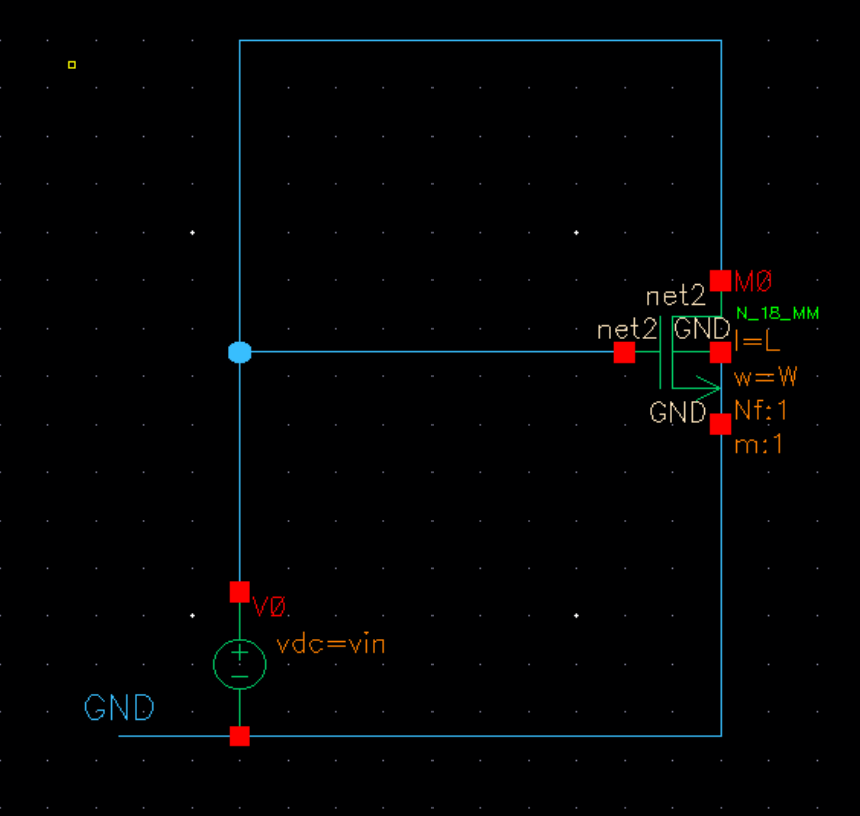
1初步仿真流程和操作
- 点击左上角
Launch-ADE Explorer新建一个maestro的仿真参数文件 - 在打开的
maestro界面的左侧右击Design Variables后点击copy from Cellview将参数设置如下
| L | 1u |
|---|---|
| vin | 2 |
| W | 1u |
- 同样的在右侧右击
Analyses,按图设置参数完后找到最右边的绿色三角开始仿真
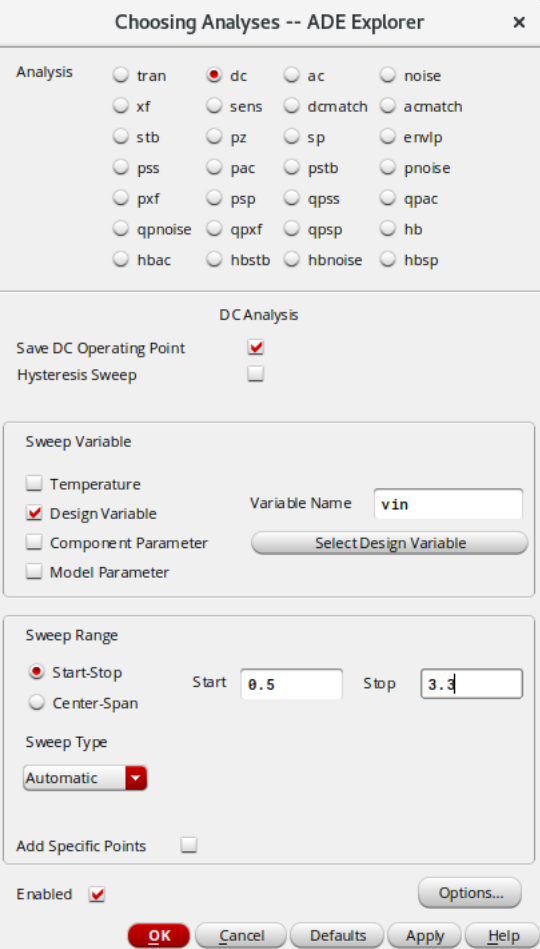
- ==这里可直接跳到第5步,直接查看所有的仿真结果==,点击最上面的
Result-Direct Plot-Main Form,在版图右键空白处,在弹出的菜单中勾选Annotations-DC Operating Points再在同一菜单点击setup按下图所示添加region,gm两个变量
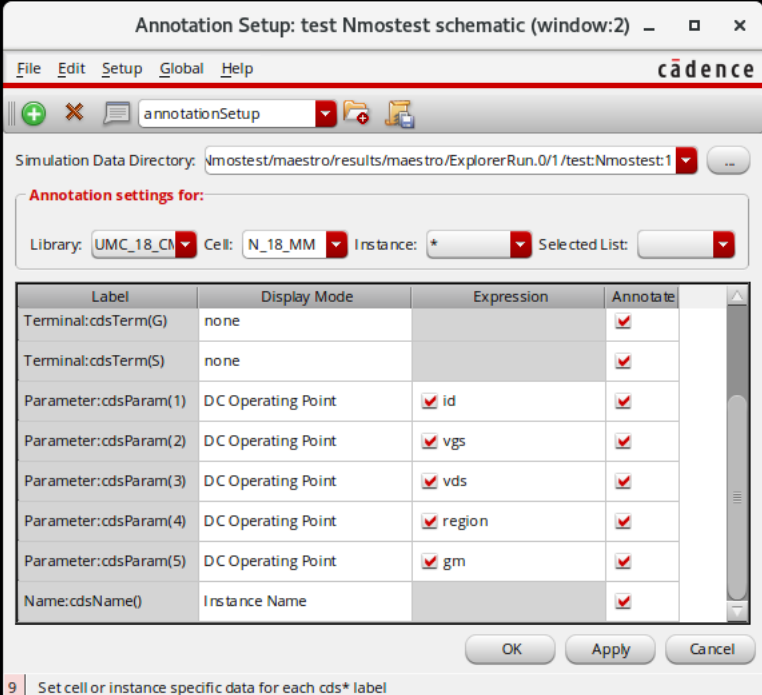
- 回到liunx界面文件管理中在Cadence的启动文件夹打开终端,输入
1 | touch savedc.scs |
后在创建的文件savedc.scs中写上save M0:all
- 在Cadence中
maestro界面上面工具栏点击setup-Model Liebrary添加刚才写的savedc.scs - 在
maestro界面工具栏中点击tools-Results Browser,弹出的界面左侧,如图所示上面的文件夹代表要选择的仿真类型,这里我们选择dc;下方代表要查看的具体变量
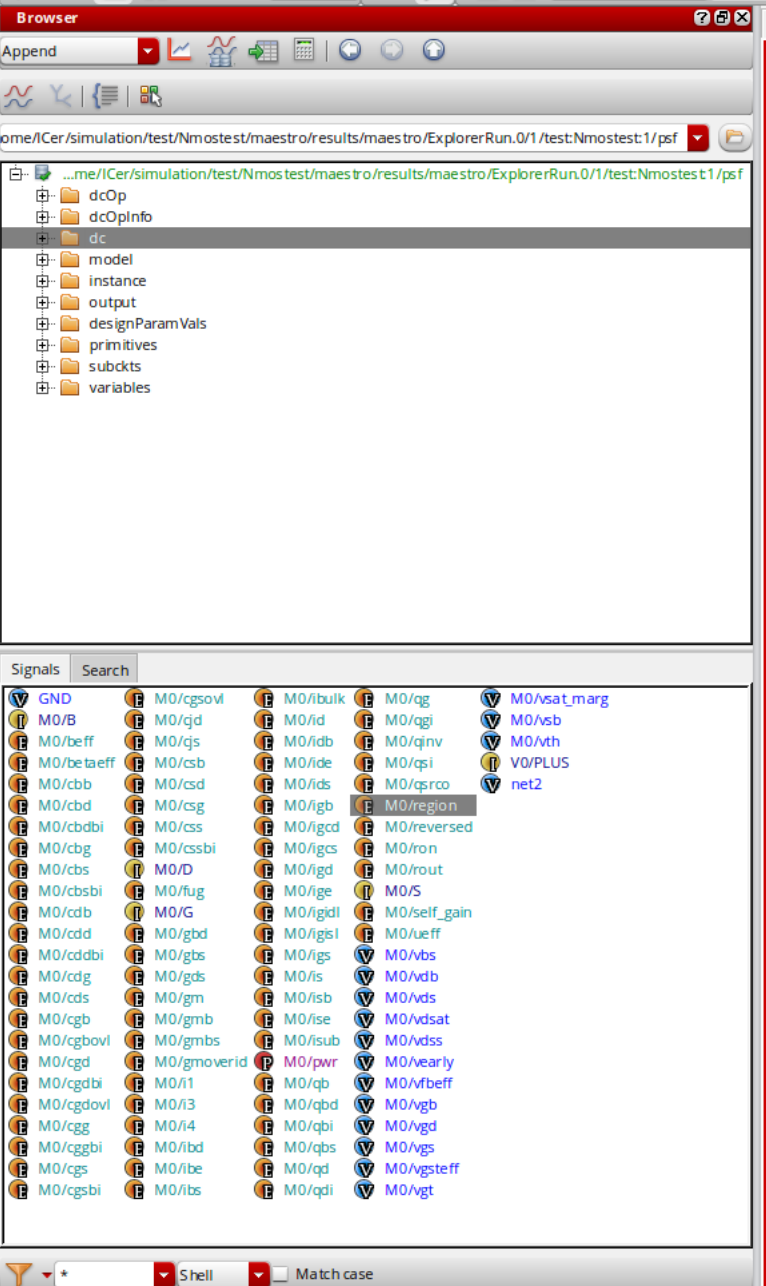
- 依次右击下方的变量
M0/self_gain,M0/id,M0?gmoverid,选择calculator,在弹出的界面中
点击齿轮图标,可以把上面三个参量固定在`maestro`界面
在maestro界面左侧将L后面的值改为一下格式:
1 | 1u:1u:10u {起点值}:{间隔}:{终点值} |
可以让仿真从L为1u开始每隔1u一直仿真到10u
2仿真计算$f_t$
$$
f_t=\frac 1{2\pi} \cdot \frac {g_m}{C_{gs}}
$$
将$f_t$的各参数如:gm,cgs送到calculator中,并按照上面给出的公式在calculator写出:
1 | ((0.5 / pi) * (getData("M0:gm" ?result "dc") / (- getData("M0:cgs" ?result "dc")))) |
后点击齿轮将其送到maestro界面
3仿真计算$V_{OV}$
$$
V_{OV}=V_{gs}-V_{th}
$$
同样的将vgs,vth等参数送到calculator
写出:
1 | v("M0:vgs" ?result "dc")-v("M0:vth" ?result "dc") |
后点击齿轮将其送到maestro界面
4绘制$V_{OV},gmid$和$f_t$图像
在maestro界面的工具栏点击Outputs-Add-Expression添加一个新的表达式
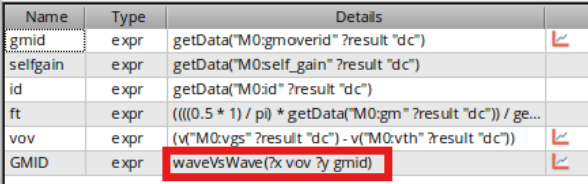
在上图Details中添加:
1 | waveVsWave(?x vov ?y gmid) |
点击仿真即可表达一个x轴是vov,y轴是gmid的图像
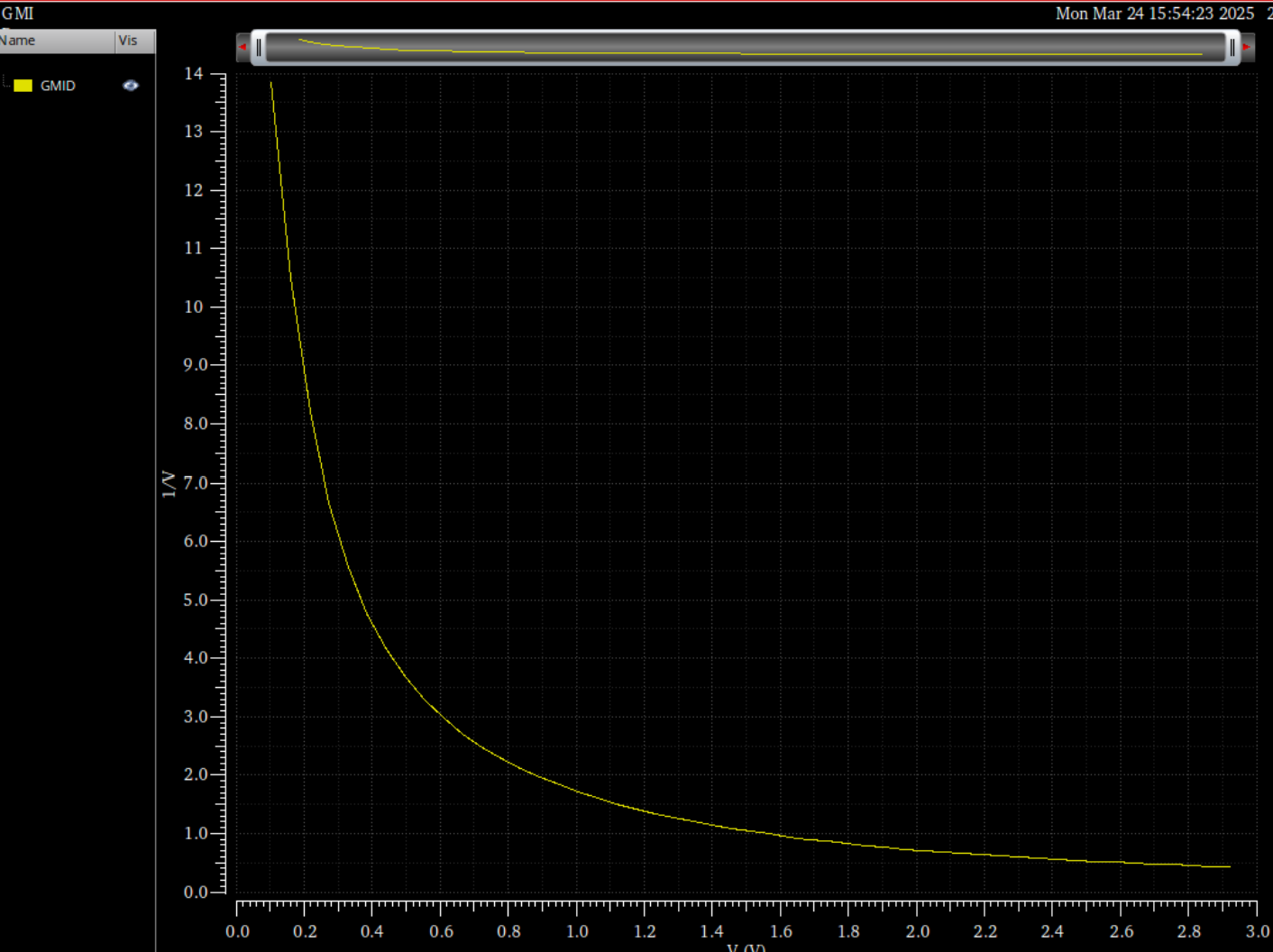
同样的绘制x轴是vov,y轴是ft的图像,输入:
1 | waveVsWave(?x vov ?y ft) |
5管子性能折中的重要参量FOM以及其余参数
我们新定义一个参量叫FOM:
$$
FOM=f_t \cdot \frac {g_m}{i_d}
$$
同样的在在maestro界面的工具栏点击Outputs-Add-Expression添加一个新的表达式:
1 | FT*GMID |
其所代表的图像如图:
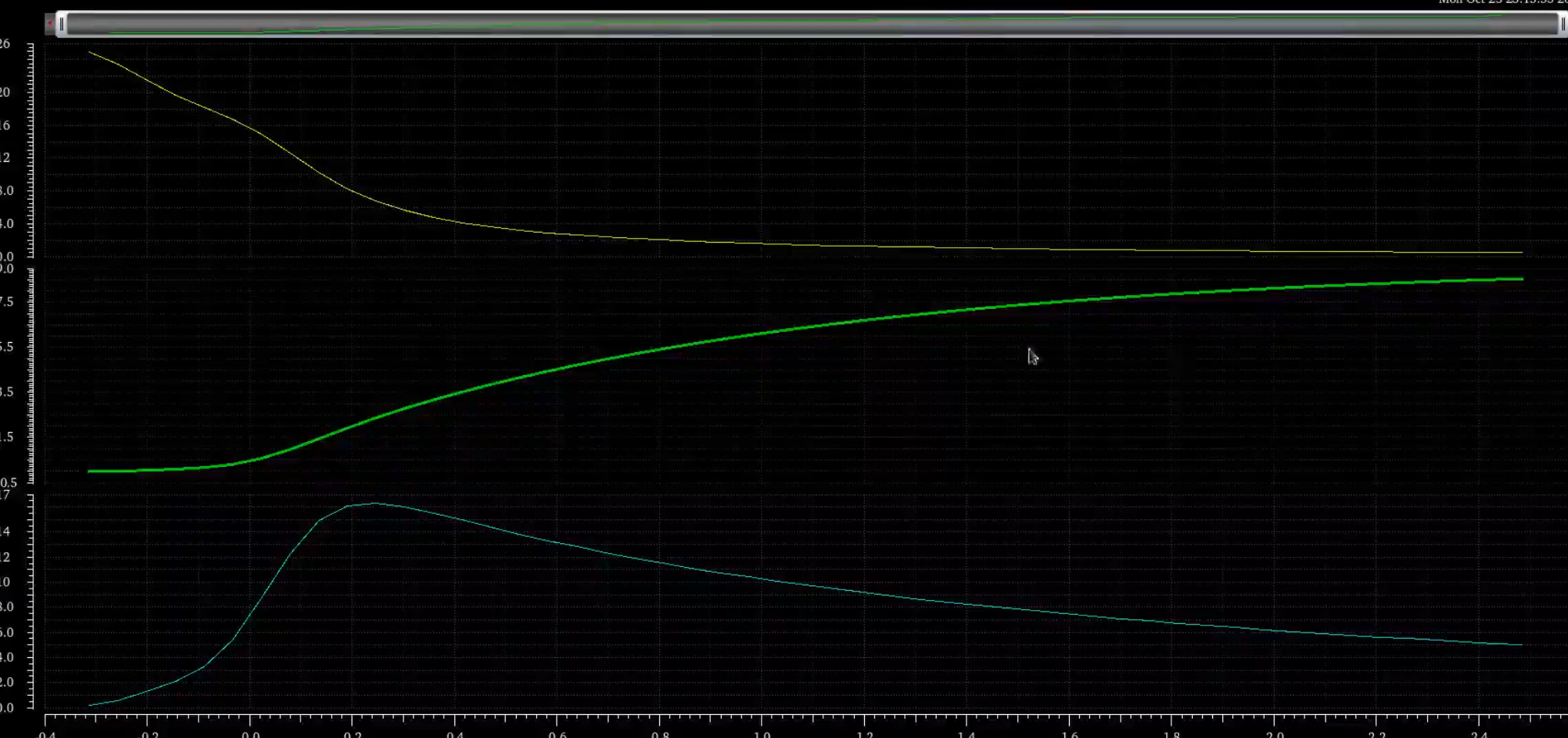
一般FOM无论什么工艺基本上在$V_{OV}=0.2V$附件取得最大值,此时管子速度和电流效率均取得较好的折中,在其他地方如下表:
| $V_{OV}变化情况$ | 性能影响 |
|---|---|
| 在极值点左侧变小 | 电流效率gmid变好,管子速度ft变差 |
| 在极值点右侧变大 | 电流效率gmid变差,管子速度ft变好 |
所以我们一般FOM取0.02V,同样的将selfgain和id跟gmid的坐标图仿真出,依次输入:
1 | waveVsWave(?x gmid ?y selfgain) |
实操——如何设计管子尺寸
假设我们要设计一个运放满足:$A_v >80dB,GBW=10MHz,C_L=2pF,PM>60$
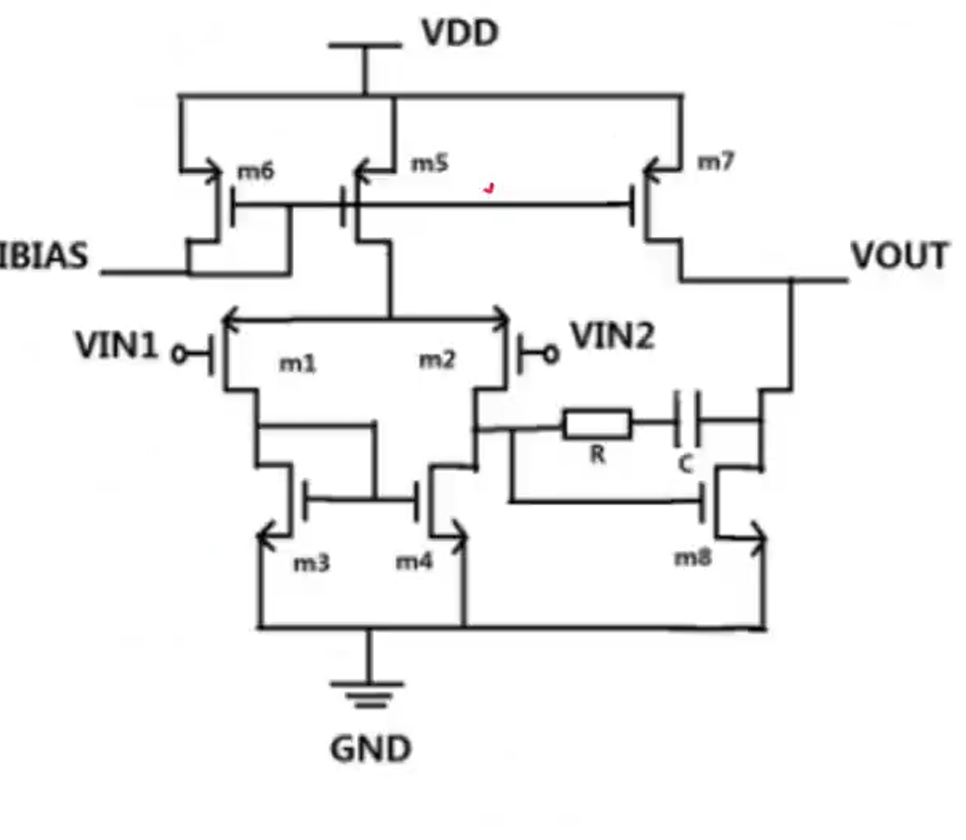
对于这个运放,要实现主极点$P_1$在带内,即GBW点内;次极点和零点在带外,我们在m8管的漏端和栅端加一个米勒补偿电容$C_c$,可以使主次极点向外推,有:
$$
P_1=\frac 1{R_{OUT1}(1+A_2)C_C}
$$
$$
P_2=\frac {g_{m8}}{C_L}
$$
$$
Z=\frac {g_{m8}}{C_C}
$$
继续计算GBW,即增益为0的点:
$$
GBW=P_1 \cdot A_{Vall}=P_1 \cdot A_1 \cdot A_2
$$
由于$A_2$很大,在下式分母中$1+A_2 \approx A_2$:
$$
GBW=\frac {A_1 \cdot A_2}{R_{OUT1}(1+A_2)C_C}=\frac {A_1}{R_{OUT1}C_C}=\frac {g_{m1}}{C_C}
$$
1决定米勒电容$C_C$的值
由于$GBW>>10P_1$,在相位图中极限情况下GBW和$P_1$相位是90度,由于我们总共有180度的相位,在经过主极点后只有90度的相位剩余,要求$P_2,Z$的相位小于90度,按照以下经验设计$P_2,Z$两点的位置:
$$
P_2=3GBW,Z=6GBW
$$
带入公式有:
$$
P_2=\frac {g_{m8}}{C_L}=3GBW=\frac {3g_{m1}}{C_C}
$$
$$
Z=\frac {g_{m8}}{C_C}=6GBW=\frac {6g_{m1}}{C_C}
$$
化简后可解得:$C_C=\frac 12C_L=1pF$可知$C_C$的取值是根据要把零极点拉的多开决定的
2确定selfgain的值
由于:
$$
A_{Vall}=A_1 \cdot A_2=g_{m1}(r_{o2}||r_{o4})\cdot g_{m8}(r_{o7}||r_{o8})>80dB
$$
在这里假设$r_{o2} \approx r_{o4},r_{o7} \approx r_{o8},80dB=10000$化简可得:
$$
A_{Vall}=\frac {g_{m1}r_{o2}g_{m8}r_{o8}}{4}=\frac {M_{2selfgain}M_{8selfgain}}{4}>10000
$$
可得:
$$
M_{2selfgain}M_{8selfgain}>40000
$$
3确定$g_{m1},g_{m8}$的值:
根据要求$GBW=10MHz$,可求:
$$
\frac {g_{m1}}{C_C}=10MHz
$$
带入计算可得$g_{m1}=63 \mu s$
由:
$$
Z=\frac {g_{m8}}{C_C}=6GBW=\frac {6g_{m1}}{C_C}
$$
可得$g_{m8}=6g_{m1}=378 \mu s$
3.选取gmid的值确定W和L的值
$g_{m8},g_{m1}$都是输入管,对于输入管有经验值可以使FOM最大:
$$
\frac {g_m}{i_d} \approx 10,11,12
$$
在这里我们取$gmid=10$,根据上一步中$g_m$的值计算得:
$$
i_{id1}=\frac {379}{10}=37.8 \mu A
$$
$$
i_{id8}=\frac 16 \cdot 37.8=6.3 \mu A
$$
这时候要确定管子的L要在Cadence中进行扫参,先建立一个Pmos的扫参数仿真图,如下图
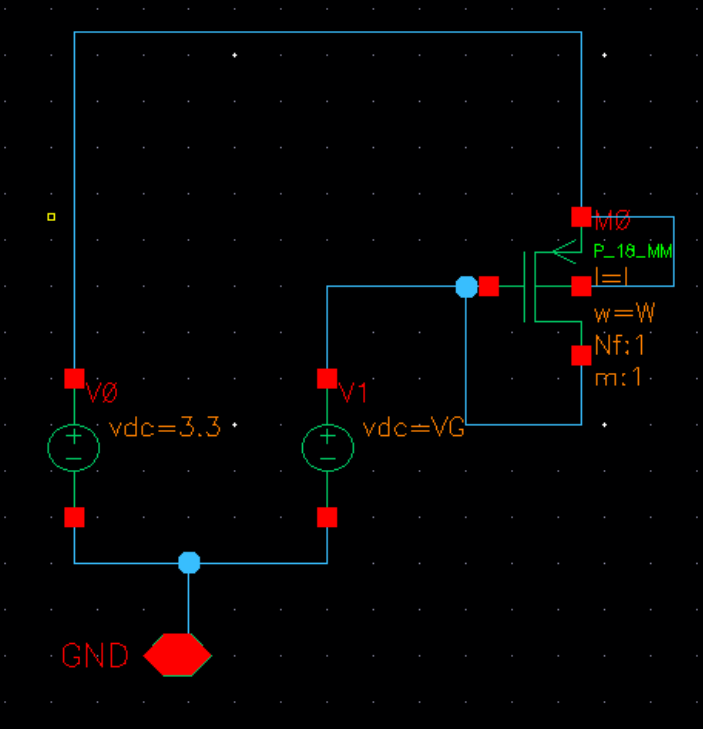
决定L的值要仿真两个重要参数,如下:
1 | waveVsWave(?x gmid ?y selfgain) |
1.L值的确定:
根据waveVsWave(?x gmid ?y selfgain)仿真出的图像,在图中找到横坐标gmid=10的地方
- 此时pmos仿真图中纵坐标selfgain大约为176,这条曲线代表的$L=1.2 \mu m$
- 此时nmos仿真图中纵坐标selfgain大约为366,这条曲线代表的$L=0.8 \mu m$
两个selfgain相乘大于前面的条件:
$$
M_{2selfgain}M_{8selfgain}>40000
$$
符合设计要求
2.W值的确定
此时对于nmos他的L已经确定,将maestro界面中L改为800n,根据仿真waveVsWave(?x gmid ?y id)的图像定W
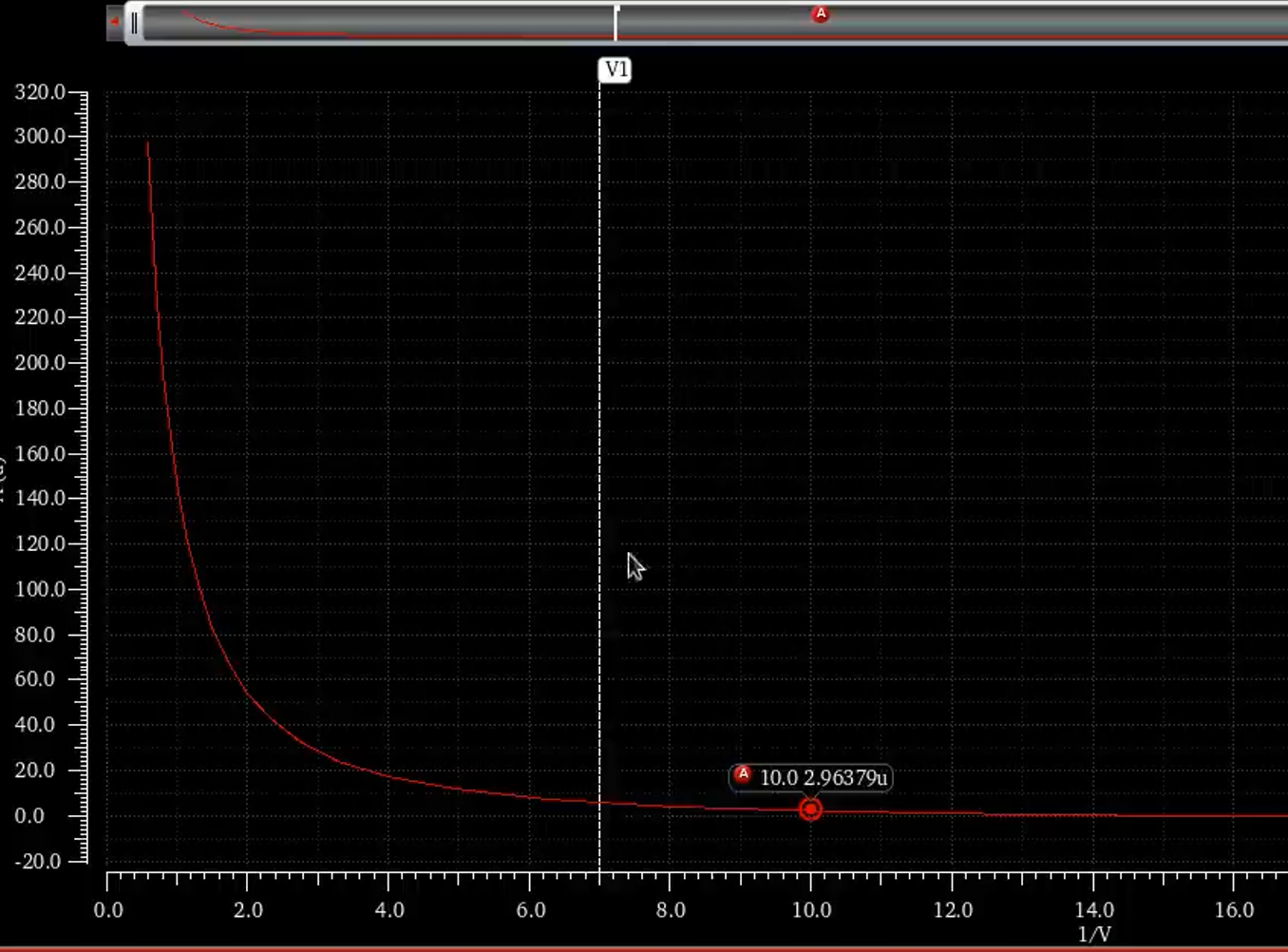
在图中选定点按A或者B,后按Q,将x轴坐标定在10,此时W=1u对应的电流为$2.96 \mu A$,在前面我们算得,需要的电流为$37.6 \mu A$,由:
$$
37.6 \mu A /2.96 \mu A \approx13 \mu
$$
也就是说当$W=13 \mu m$时,nmos管才能提供我们所需要的电流,同样的在pmos仿真中,取得$W=8 \mu m$
4.其他管子尺寸的确定
对于尾电流源$M_{5,6,7}=2 \mu m$,因为一个理想电流源内阻趋近于无穷,故我们将其L取得很大,其内阻也会很大,切合电流源的需求;按照经验值我们将其的gmid=8
- 对于$M_6,I_{BIAS}=2 \mu A$同样的在
waveVsWave(?x gmid ?y selfgain)仿真图中gmid=8,I=0.7 \mu A,在这里我们近似取$I_{BIAS}=2.1 \mu A$,可以近似得到$W=3 \mu m$ - 对于$M_5$,两个输入pmos电流相加等于流过它的电流约等于$12 \mu A$,这电流相当于上面$M_5$的6倍,有$W=3 \cdot 6 =18 \mu m$
- 对于$M_7$,下面输出管$I_{M_8} \approx 36 \mu A$,约为$M_5$的3倍,有$W=3 \cdot 18=54 \mu m$
i对于$M_{3,4}$,由于$M_8$的的栅极电压在共模下实际上就是$M_{3,4}$的栅极电压,要保证第二集不进入线性区,故他们的gmid应该相同;$M_{3,4}$流过的电流为$\frac 16I_{M_8}$,故其$W_{3,4}=\frac 16 13 \mu m \approx 2\mu m$