LDO全称低压差线性稳压器

- 其通过使用在线性区域内运行的晶体管或者场效应管,通过调节晶体管或者场效应管两端的电压,产生经过调整的输出电压
- 但其只能使用降压应用中,$V_{out}<V_{in}$
LDO的一些功能
- 直流转交流:将220V交流市电转化稳定的直流电压
- 稳定电池电压:电池电压会随着电量而变化,LDO能将其输出的电压稳定在一个固定值上
- 减小输出纹波:在DCDC模块后消除其输出电压的波动
1一个基本的LDO电路
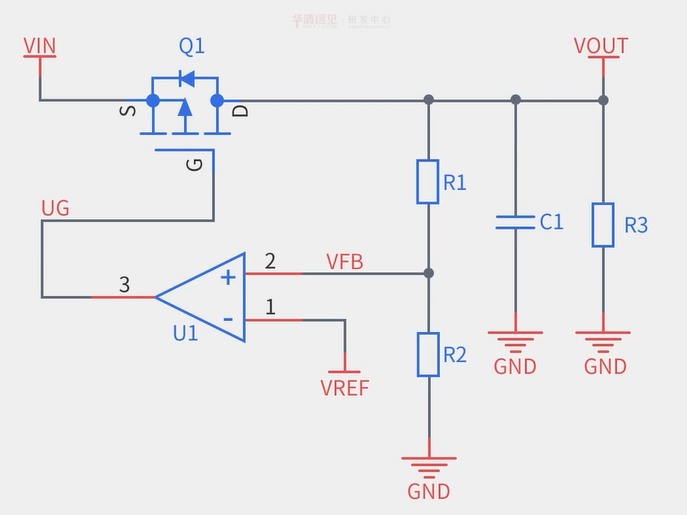
1.1电路组成和原理
1.1.1组成
- 分压取样电路
- 基准电压:$V_{ref}$(带隙基准BGR产生的一个不受温度影响的零温度系数电压)
- 误差放大电路:运算放大器OPA,总是倾向于使得正(+)负(-)输入端的电压相等,当$V_{FB}<V_{ref}$时,运放就会减小输出
- 晶体管调整电路
1.1.2负反馈调节稳压的原理
由运算放大器的虚短虚断将$V_{ref}$从‘+’端引到‘-’端:
$$
V_{ref}=V_-=V_+
$$
根据电阻分压得:
$$
V_{out} \cdot \frac {R_1} {R_1+R_2}=V_{ref}
$$
进一步的:
$$
V_{out} =V_{ref}\cdot \frac {R_1+R_2}{R_1}
$$
可以看到$V_{out}$实际上是由$V_{ref}$放大得来的,通过$R_1,R_2$和运放组成的负反馈分压结构将$V_{out}$稳定在与$V_{ref}$相关联的一个固定值,从而==实现了当负载电压发生变化时通过反馈回路来控制晶体管两端电压,使输出保持恒定不变==
1.输出电压增大时
当$V_{out}$增大时,$V_{FB}$相应增大,由放大器$U1$对误差放大,故$UG$增大;若此时$V_{in}$保持不变,对于晶体管两端
$$
|V_{gs}|\downarrow =|V_{in}|-|UG| \uparrow
$$
根据晶体管在饱和区有:
$$
I_D \downarrow = \frac 12 \mu_n C_{ox}\frac WL(V_{gs} \downarrow-V_{thp})^2
$$
$I_D$减小,$R_3$上分得的电流减小,分得的电压也相应减小,故$V_{out}$减小,调整到原理稳定的状态
2.输出电压减小时
当$V_{out}$减小时,$V_{FB}$相应减小,由放大器$U1$会减小其的输出==(总是倾向于使得正(+)负(-)输入端的电压相等,当$V_{FB}<V_{ref}$时,运放就会减小输出)==,故$UG$较小;若此时$V_{in}$保持不变,对于晶体管两端
$$
|V_{gs}|\uparrow =|V_{in}|-|UG| \downarrow
$$
根据晶体管在饱和区有:
$$
I_D \uparrow = \frac 12 \mu_n C_{ox}\frac WL(V_{gs} \uparrow-V_{thp})^2
$$
$I_D$增大,$R_3$上分得的电流增加,分得的电压也相应增大,故$V_{out}$增大,调整到原理稳定的状态
2LDO的重要性能指标
2.1压差$V_{drop-out}$

如上图所示$V_{drop-out}$即压差,==是指正常稳压所需的$V_{IN}-V_{OUT}$的最小差值==
| 情况 | 工作状态 |
|---|---|
| $V_{IN}-V_{OUT}>V_{drop-out}$ | LDO电路正常工作 |
| $V_{IN}-V_{OUT}<V_{drop-out}$ | 由于功率管处于线性区,LDO对$V_{OUT}$失去调节作用,反馈环路不稳定 |
$V_{drop-out}$可以用以下公式表达:
$$
V_{drop-out}= I_{POWER} \cdot r_{ds}
$$
其中:
- $I_{POWER}$是功率管上通过的电流
- $r_{ds}$是功率管的等效电阻
还需要注意的是,$V_{drop-out}$还会受到$V_{IN}$,功率管种类尺寸,温度等因素影响,==但通常来说更小压差代表LDO的效率更高==;故一般来说,要把一个$9V$的电压转化为$3.3V$,我们通常取一个中间电压来提升LDO电路的效率
2.1静态电流$I_Q$
是指LDO工作在稳态情况下,$I_Q$有:
$$
I_Q = I_{IN} - I_{LOAD}
$$
其中:
- $I_{IN}$是由$V_{IN}$提供的LDO工作所需要的电流大小
- $I_{LOAD}$负载电流
在习惯上,一般认为静态电流为LDO空载时消耗的电流,此时$I_{LOAD}=0$,上面的公式可改写为:
$$
I_Q = I_{IN}
$$
误差放大器是主要消耗静态电流的模块
2.2效率$\eta$
是指LDO输出与输入功率之比,有:
$$
\eta = \frac {I_{OUT}V_{OUT}}{(I_{OUT}+I_Q) \cdot V_{IN}}…式1
$$
$I_Q$越小$\eta$越高,当$I_Q$足够小时,即$I_{OUT}>>I_Q$,上式可改写为:
$$
\eta = \frac {V_{OUT}}{V_{IN}}…式2
$$
观察上面的公式:
| 工作状态 | 影响效率的主要因素 | 为什么? |
|---|---|---|
| 工作时 | $V_{drop-out}$ | 由式1,$V_{drop-out}$越小,代表$V_{OUT},V_{IN}$的差值越小,$\eta$的分子分母的值将接近,故效率越高 |
| 空载时 | $I_Q$ | 由式2,$I_Q$越小$\eta$越高 |
2.3负载调整率LDR
是输出电流变化时,输出电压维持在标称值上的能力衡量,代表了LDO电路的大信号调节能力,有:
$$
L D R=\frac{\Delta V_{OUT }}{\Delta I_{OUT } V_{OUT }}
$$
我们一般使用的PMOS管LDO:
$$
\Delta I_{OUT }=\Delta V_{OUT } \frac{R_{F 2}}{R_{F 1}+R_{F 2}} A_{v, EA} \cdot g_{mP}
$$
其中:
- $\Delta V_{OUT }$是输出电压变化量
- $\Delta I_{OUT }$指负载电流变化量
- $A_{v, EA}$指误差放大器的低频增益
- $g_{mP}$指PMOS功率管的跨导
进一步的,两边同除$\Delta V_{OUT}$可得:
$$
\frac {\Delta I_{OUT }}{V_{OUT}}= \frac{R_{F 2}}{R_{F 1}+R_{F 2}} A_{v, EA} \cdot g_{mP}
$$
由上述两式可以得到:
$$
L D R=\frac{1}{V_{OUT }} \frac{1}{A_{v, EA} g_{mP}} \frac{R_1+R_2}{R_2} × 100
$$
由此可知,负载调整率可由提高LDO的误差放大器低频增益,增大功率管宽长比得到改善。
2.4线性调整率
是当输入电压变化时,输出电压维持在标称值上的能力,也是代表了LDO电路的大信号调节能力,表示为:
$$
LNR=\frac{\Delta V_{OUT }}{\Delta V_{IN} V_{OUT }}…式1
$$
当输入电压变化引起输出电压变化时,$\Delta V_{\mathbb{N}}$与$\Delta V_{OUT }$有如下关系:
$$
\frac{\Delta V_{OUT}}{\Delta V_{IN}}=\frac{1}{A_{v, EA} \cdot g_{mP}\left(r_{ds}+R_{LOAD}\right)} \frac{R_{F 1}+R_{F 2}}{R_{F 2}}…式2
$$
其中:
- $\Delta V_{IN}$是输入电压变化量
- $R_{LOAD }$是负载电阻大小
将式2代入式1,可以得到:
$$
LR=\frac{1}{V_{OUT}} \frac{1}{A_{v, EA} g_{mP}\left(r_{ds}+R_{LOAD}\right)} \frac{R_{F 1}+R_{F 2}}{R_{F 2}} × 100 %
$$
观察上式线性调整率也可由提高LDO的误差放大器低频增益得到改善
2.5电源抑制比
电源抑制比PSRR表示为:
$$
PSRR = 20lg\frac{\Delta V_{OUT}}{\Delta V_{IN}}
$$
电源抑制比可看作输入电压$V_{IN}$到输出电压$V_{OUT}$的增益,单位为dB,随频率变化而变化。表征输出电压对输入电压噪声及纹波的抑制能力
PSRR绝对值越大代表LDO对输入电压噪声及纹波的抑制能力越强,也是LDO具有“干净”输出电压的重要原因之一
在LDO中,电源抑制比通常与基准电压源的PSRR,EA的低频增益,系统零极点位置以及个数有关。
2.6时域响应
在LDO电路中,随着负载的增大和减小,有下表的变化:
| 负载电流$I_{LOAD}$变化 | 电路内部变化 | $V_{OUT}$ |
|---|---|---|
| 增大 | 功率管的更多电流会流向负载,$R_1,R_2$;负载分得的电流减小 | 下降,出现下冲 |
| 减小 | 功率管的更多电流会流向$R_1,R_2$;负载分得的电流减小 | 上升,出现上冲 |
对于下冲电流有:
$$
I_{dip}=\frac {ΔI_{OUT}}{2πRC_L}⋅Δt
$$
乘上电阻R可以得到下冲电压:
$$
V_{dip}=\frac {ΔI_{OUT}}{2πC_L}⋅Δt
$$
其中:
- $Δt$是稳定值到最高或者最低值的时间
- $C_L$是片外电容的容值
Δt可以由下面公式得出:
$$
\Delta t = \frac{1}{BW}+2\pi \frac{C_g\Delta V_g}{I_{SR}}
$$
其中:
- $BW$为带宽
- $C_g$是功率管栅极的寄生电容
- $\Delta V_g$是功率管调整变化电流,所需的电压
- $I_{SR}$是压摆率
故有片外电容的时候,我们常常用使$C_L$尽可能大来控制$V_{dip}$;无片外电容时,我们常常用$Δt$中$BW,Cg,ISR$来控制
3LDO设计的设计原理
3.1片外电容和非片外电容
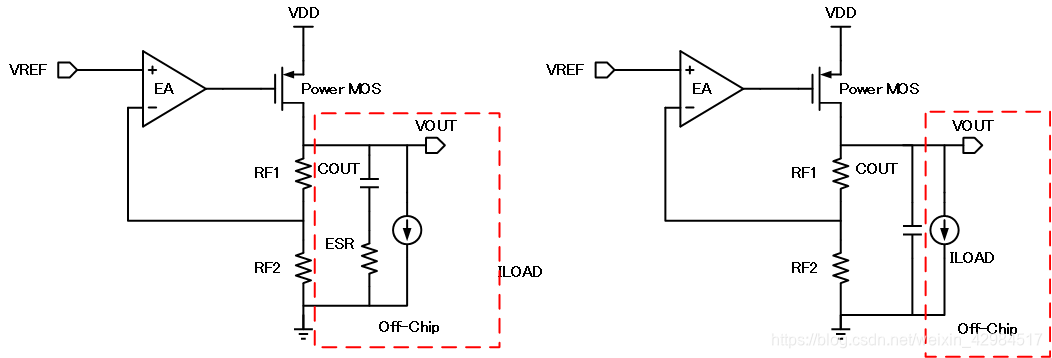
3.1.1传统有片外电容LDO稳定性分析
其最主要的特点在于 LDO 的输出电容和负载都在片外,要在输出端外接一个级别的大电容,其有两个作用:
- 可以稳压和拉低输出极点频率的功能
- 会带来一个寄生的等效串联电阻$R_{ESR}$,电阻会形成一个额外的低频零点,可以通过适当的设计该零点的频率和次主极点的频率,使得二者能做到相互抵消,以提升LDO的环路带宽和相位裕度
缺点:
- 但这种结构下,得到的LDO芯片的面积会因为较大的输出电容而增大,从而损耗更多的面积
- 由于$R_{ESR}$的存在,片外大电容$C_{L}$无法对负载的突然变化做出跟随影响,因为其无法瞬间靠压差产生一个大电流,于是还需要在片内加入一个容值较小的高频稳压电容$C_A$

其中:
$C_A$是高频稳压电容,和反馈电阻$R_1,R_2$均处于片上
$R_L$是负载电阻,是LDO负载电路的等效电阻,用以模拟负载端对LDO的电流需求
$C_L$为级$\mu F$别的片外的大负载电容,$R_{ESR}$是指其等效串联电阻
| 零极点情况 | 形成原因 |
|---|---|
| 主极点$P_1=\frac 1{R_LC_L}$ | 传统LDO的输出电容极大,那么和输出阻抗也会产生一个极点;且由于输出电容$C_L$是$\mu F$级别,栅极寄生电容是$C_g$是$pF$级别,故这个极点为主极点 |
| 次极点$P_2=\frac 1{R_{EAout}C_g}$ | 由于较大的误差放大器增益所要求的电阻$R_{EAout}$和功率管较大带负载需求导致功率管的$\frac WL$较大,所带来的寄生电容$C_g$组成的频率第二低的次主极点 |
| 零点$Z=R_{ESR}C_{OUT}$ | 是由输出端的输出电容和ESR电阻产生,可以通过调整片外电容$C_L , R_{ESR}$的值改变零点的位置,同该次极点抵消,从而拉宽带宽,改善环路相位裕度 |
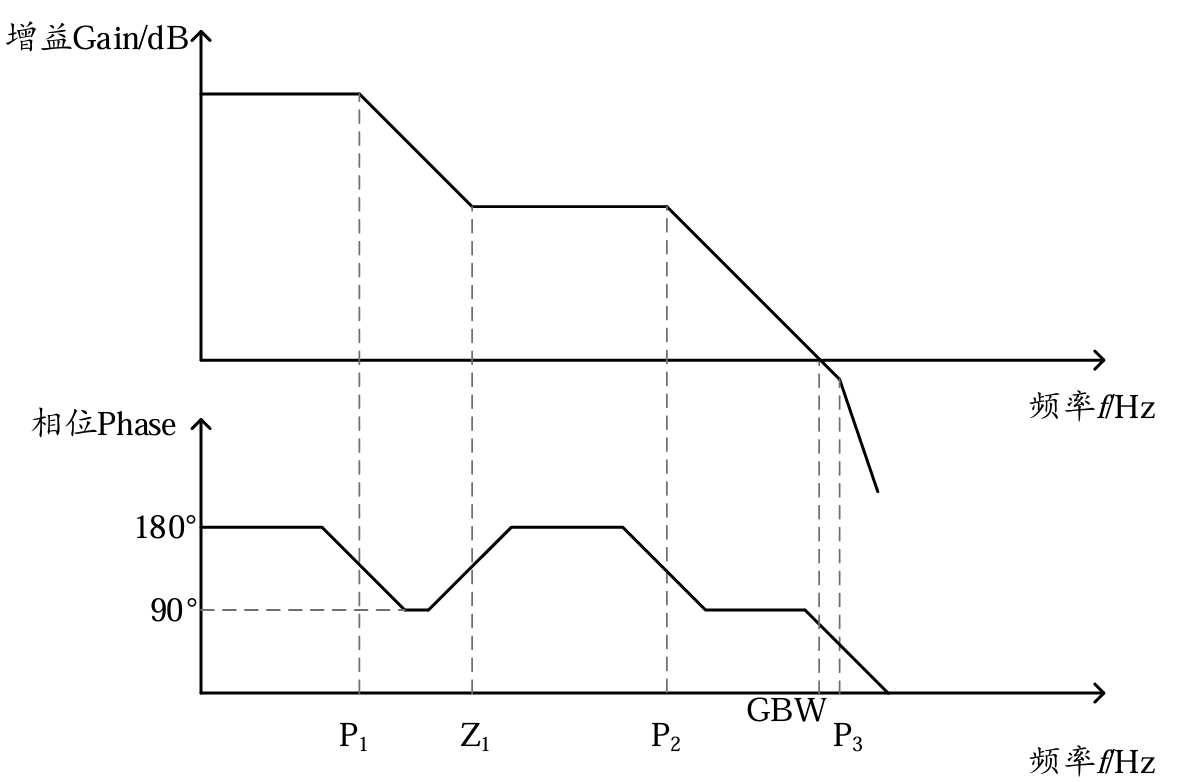
对于传统的LDO而言,当负载越来越大的时候,得到的等效输出电阻$R_L$会进一步变小,导致主极点$P_1$向高频(即上图右端)移动;当主次极点过于接近时,如无ESR 点存在(其中Z1和P2作用相互抵消,增加了带宽),相位裕度将会恶化,环路稳定失效,故整个LDO系统的稳定性会随着负载的增大而变差
3.1.2无片外电容LDO稳定性分析
由于需要片上集成因此:
- 无法在输出引脚上加上外接的片外大电容,其所有需要的器件都必须将大小控制在可以集成于芯片内部的水平,如电容、电阻、带隙基准电路等
- 可以看出输出端仍有稳压电容$C_L$,不过此时$C_L$大小仅有$pF$级别,最大不超过$nF$级别,并且是集成于片上的。
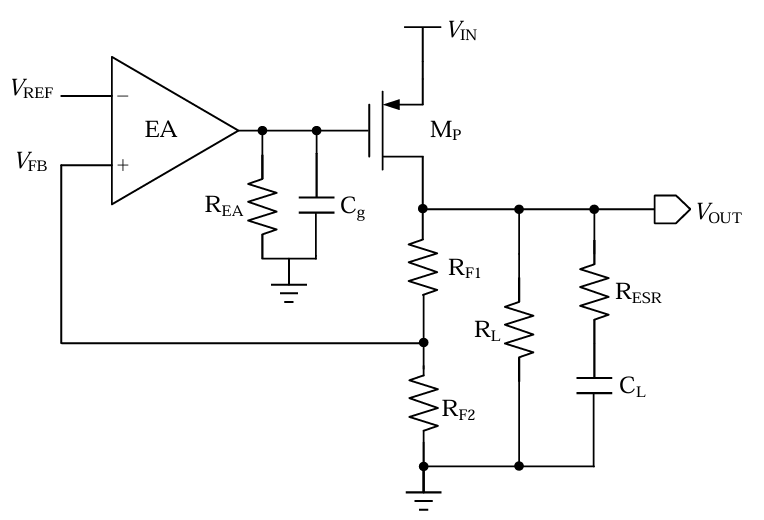
| 零极点情况 | 形成原因 |
| 主极点$P_1=\frac 1{R_{EAout}C_g}$ | 此时$C_L≈C_g$其数量级较为接近,而功率管栅极对地的等效输出阻抗$R_{EA}$远大于最后一级输出端的等效输出阻抗$R_L$,故主极点从LDO的输出端变为$\frac 1{RC}$数值更小的功率管的栅极 |
| 次极点$P_2=\frac 1 {R_LC_L}$ | |
| 无零点存在 |

如上图所示,对于无片外电容的LDO而言其LDO的相位裕度将足够大,环路将十分稳定,但稳定性受稳压电容$C_{L}$大小的影响,由:
$$
P_{2} = \frac{1}{R_{L}C_{L}}
$$
- 当稳定电容增大时$C_{L}\uparrow$,$P_{2} = \frac{1}{R_{L}C_{L}\uparrow}\downarrow$,次极点$P_{2}$会靠近主极点,使得环路稳定性变差
- 当稳定电容过小时$C_{L}\downarrow$,$P_{2} = \frac{1}{R_{L}C_{L}\downarrow}\uparrow$,虽然极点被推远,但当负载瞬态变化的时候,就没有足够大的电容为其短暂提供/吸收电荷,会使得其有着更大的过冲/下冲电压幅度
3.2频率补偿方式
3.2.1 动态零点补偿技术
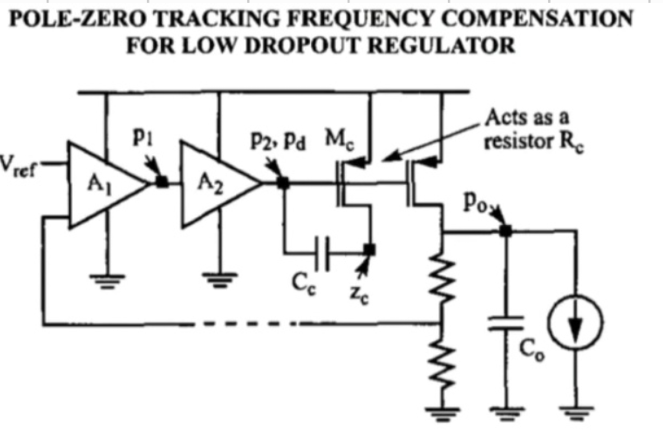
对于$M_{c}$这个$Pmos$,D端接$C_{c}$其上面几乎无电流,$M_{c}$工作在深线性区,其相当于一个电阻:
$$
R_{c} = \frac{1}{k’\frac{W}{L}(V_{gs} - V_{th})
}
$$
又因为$Pmos$管$M_{c},M_{p}$栅极接在一起,其具有相同的$V_{gs}$,由上面的公式可以看到,$R_{c}$会随着$V_{gs}$变化,$R_{c}$可看作一个等效电阻。
1.其会引入一个零点,是由于对于管$M_{c},C_{c}$的并联,其相当于管内阻$R_{c}$与$C_{c}$串联,根据$RC$法估计,零点的表达式为:
$$
Z_{c} = \frac{1}{R_{c}C_{c}}…式1
$$
2.次极点位于输出端:
$$
P_{0} = \frac{1}{r_{0}C_{o}}
$$
再带入管的内阻公式$r_{0} = \frac{1}{\lambda I_{LOAD}}$带入上式中:
$$
P_{0} = \frac{\lambda I_{LOAD}}{C_{0}}…式2
$$
根据式1和2,为了使零点$Z_{c}$能够较好的补偿跟随零点$P_{0}$,电容$C_{c}$的值要接近甚至大于$C_{o}$的数量级。
3.在$P_{D}$处:
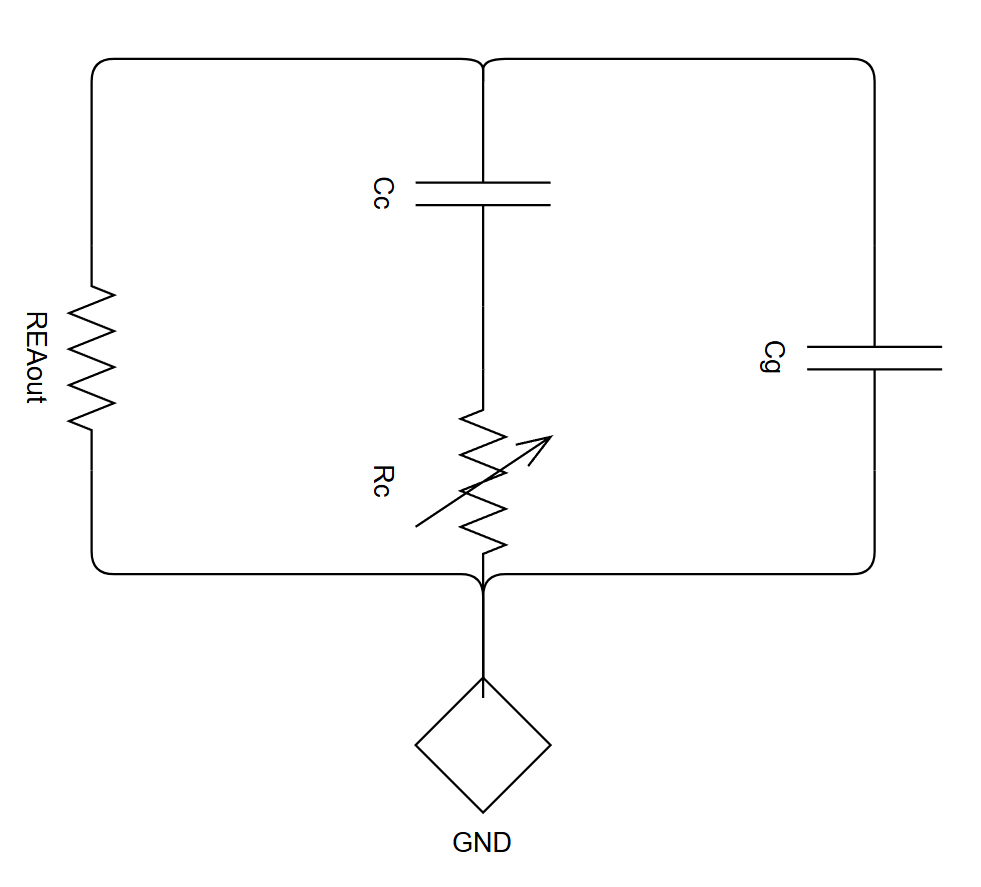
对$C_C$上KCl:
$$
\frac{1}{R_{EA}} + \frac{1}{SC_{c}} + R_{c} + SC_{g} = 0
$$
化简:
$$
SC_{c}R_{C} + 1 + SC_{c}R_{EA} + SC_{g}R_{EA}(SC_{c}R_{c} + 1) = 0
$$
$$
S^{2}C_{g}C_{c}R_{EA}R_{C} + SC_{g}R_{EA} + SC_{c}R_{EA} + SC_{c}R_{c} + 1 = 0…式3
$$
利用主极点近似,一定能化为如下这种结构:
$$
(1 - \frac{S}{P_{2}})(1 - \frac{S}{P_{D}}) = 0
$$
我们设$P_{D}$为主极点,即$|P_{2}| > |P_{D}|$,将上式乘开:
$$
1 - \frac{S}{P_{D}} + \frac{S^{2}}{P_{2}P_{D}} = 0
$$
与式3对比可解得:
$$
P_{D} = \frac{1}{C_{g}R_{EA} + C_{c}R_{EA} + C_{c}R_{c}}
$$
根据前面我们的分析
为了使零点$Z_{c}$能够较好的补偿跟随零点$P_{0}$,电容$C_{c}$的值要接近甚至大于$C_{o}$的数量级
可得$C_{g} \gg C_{c}$,继续化简上式,约去含$C_{c}$的项,可以得到主极点:
$$
P_{D} = \frac{1}{C_{c}(R_{EA} + R_{c})}
$$
$C_{c}$要大,主极点$P_{D}$才能小,才能成为主极点,这也与我们上面分析$C_{c}$本身自己的值要大相符合,再继续解得次极点:
$$
P_{2} = \frac{1}{R_{c}||R_{EA}}
$$
但上述的方法通过增大$C_{c}$的值来实现零点跟随补偿,会带来一个问题,越大的电容容值其在版图上所占面积越大

原理跟上文一样,但其通过设计缓冲器,将$P_{N1}, P_{N2}$推到高频率处,通过Buffer隔离:
- 使得输入寄生电容由$C_{p}$变为$Cib$,减小了输入电容
- 使输出电阻由$r_{o},R_{EA}$变为了$r_{ob}$,减小了输出电阻
- 通过设置零点去跟随单位增益频率带宽的频率点,与上文相比,由于其零点大得多,$C_{c}$可以小得多
$P_{c}$上面我们已经推到过,直接套用:
$$
P_{c} = \frac{1}{(R_{EA} + R_{z})C_{c}}
$$
由于$C_{c}$较小,且等效可调电阻$R_{z} \ll R_{EA}$,虽然其仍然会受负载变化影响,但整体上,$P_{c}$不受负载影响对于主极点:
$$
P_{0} = \frac{\lambda I_{LOAD}}{C_{L}}
$$
容易受影响且会引起$UGB$的变化
3.2.2放大电路的设计原理
运放的开环增益决定了使用运放的反馈系统的精度
$$
\frac{Y}{X} = \frac{A}{1 + \beta A} \approx \frac{1}{\beta}(1 - \frac{1}{\beta A})
$$
可以看到开环增益会影响’+’和’-‘端虚短虚断的精度,当开环增益没有足够大时;在实际仿真中两端的电压并不完全相同,而是相差$0.005V$这样的数量级