半导体物理笔记第一章

波函数：粒子在某时刻某位置出现的概率，且其概率密度函数为
$$[ P(x,t) = \psi^*(x,t) \psi(x,t) = |\psi(x,t)|^2 ]$$
与时间无关的概率密度函数为
$$P(x) = \psi^*(x) \psi(x) = |\psi(x)|^2$$

1.1半导体中的电子状态

在这里我们讨论两种情况，由两种特殊情况得出半导体中的普遍规律

1.1.1孤立电子与自由电子的状态

1孤立原子

电子处于原子核的束缚状态，只含有原子核和核外电子，如

• H原子
  原子核对于电子有库伦力产生的势场
  $$V(r)=\frac{－q^2}{4\pi\epsilon_0r}$$
  电子的能量需要满足以下条件薛定谔方程才有解
  $$E_n=－[\frac{m_0q^4}{8\epsilon_0^2h^2}]\frac 1n^2，n量子数=1,2,3..$$
  其中[]为13.6于是公式可以改写为
  $$E_n=－13.6\cdot\frac 1n^2 (eV)，n=1,2,3..$$
  由上述可得出H原子核外电子状态是一系列分立（离散）的确定的能量值（能级），==可以得到孤立原子中电子的能量是不连续的，这种各个分立的能量值称为能级==
• 多电子原子
  其电子和电子有作用力称之为微拢，其核与电子有作用力
  ==其核外能量依然不连续==，量子数不再是单个n，而是有四个量子数为别为：

$n$	主量子数
$l$	角量子数
$m_l$	磁量子数
$m_s$	自旋量子数

2自由电子

给定足够的能量，电子挣脱原子核束缚成为自由电子

由一维薛定谔方程
$$
-\frac{\hbar^2}{2m} \frac{\partial^2 \psi(x, t)}{\partial x^2} + V(x) \psi(x, t)=E\psi(x, t)
$$
定态薛定谔方程
$$
-\frac{\hbar^2}{2m} \frac{d^2 \psi(x)}{d x^2} + V(x) \psi(x) = E \psi(x)
$$

$$

$$

在自由电子中
$$
V(x)=0，
可得-\frac{\hbar^2}{2m} \frac{d^2 \psi(x)}{d x^2} = E \psi(x)
$$
对后面这个二次幂函数求解
$$
\psi(x)=A \cdot e^{i2 \pi kx}，k=\frac 1\lambda
$$
由于并不像氢原子一样E有约束关系，解并不像氢原子一样是分立的，而是连续的从下面也可证得
$$
由\left{
\begin{aligned}
E=\frac {P^2}{2m_0} \
P=\hbar\cdot k
\end{aligned}
\right. 得E=\frac{\hbar^2k^2}{2m_0}
$$

• 从几何角度看，从得出的方程可以看到E和K的关系是连续的，E在坐标轴中是一个开口朝上连续的二次函数
• 从波矢角度看，由于波矢是矢量，是连续变化的，E和K的关系中除$\vec k$都是固定的数，因此$\vec k$的连续变化引起了能量的连续变化

==由此可知自由粒子的能量状态是连续的==

3半导体中的电子

半导体中的势场由以下三种组成

• 孤立原子中电子势场=原子核势场+其他电子的势场

$$
V(r)=\frac{－q^2}{4\pi\epsilon_0r}
$$

• 自由电子不受任何势场的控制

$$
V(x)=0
$$

• 半导体中电子势场不清楚，只讨论背景（严格周期性重复排列的原子间运动）
  利用单电子近似模型，即把所有电子和其所受的力看做一个整体来研究，==其有两个方面理想化：晶体（半导体）无缺陷，原子固定不动==

1.1.2分析半导体电子状态的方法——单电子近似

单电子近似模型的定义：假设==半导体中的电子是在严格周期性重复排列的（晶体无缺陷）==，且==固定不动的原子核势场（原子固定不动）==，以及大量电子的平均势场下运动

1单电子近似的意义

• 把复杂的原子核和电子混合系统中的核与电子之间的作用力加以分离
• 把众多电子相互牵制的复杂电子问题，近似看做大量电子对某个（单个）电子的影响等效为一个平均势场对电子的影响

这种用单电子近似法研究晶体中电子状态的理论称为能带论

2单电子近似的计算

根据单电子近似，周期性势场＋平均势场=周期性势场
$$
V(x)＋V(Sa)=V(x)，S整数，a晶格常数
$$

其在二维空间中是具有周期性的一维周期性势阱，再带入薛定谔方程：
$$
-\frac{\hbar^2}{2m} \frac{d^2 \psi(x)}{d x^2} + V(x＋Sa) \psi(x) = E \psi(x)，\hbar=\frac h{2\pi} \\hbar为修正普朗克常数是为了方便计算得出的
$$
为了解出上面新的$V(x+Sa)$我们要引入布洛赫定理，其是周期性势场的一维薛定谔方程的解，形式为：
$$
\psi_k(x)=u_k(x) \cdot e^{ikx} \ u_k=u_k(x+na)
$$
其中$u_k(x)$是周期性的，不是保持不变的

3结论

	自由电子	晶体中电子
波函数	$\psi(x)=Ae^{ikx}$，其中$k=\frac{2 \pi}{\lambda}$	$\psi_{k}(x)=u_{k}(x)e^{i kx}$，其中$\lambda=\frac{2\pi}k$

两者的波函数形式相似，都表示波长为$\lambda=\frac{1}{k}$，沿$k$方向传播的平面波。但晶体中用周期性调制振幅$u_{k}(x)$代替了自由电子中的恒定振幅$A$

	自由电子	晶体中电子
概率密度函数	$	\psi(x)\psi^{*}(x)
意义	是晶格常数$a(A)$的周期性函数，表示晶格中找到电子的概率具有周期性	反映了电子不再局限于某原子上，而是可以在基本原子自由运动到其近邻格胞对应位置的可能性，==也称为共有化运动，电子在每个晶胞对应点等几率出现==

1.1.3半导体中的电子能带

1准自由电子近似

设想将一个电子放在晶格中，由于晶格原子的存在，电子波在传播过程中会受到格点原子的反射

1. 一般情况：个反射波会相互抵消，对前进波无重大影响

2. 特殊情况：前进波和反射波满足一定相位关系，满足1.2中的布拉格发射条件，在
   $$
   k=\frac {n}{2a}，n=\pm1,\pm2…处
   $$
   形成驻点，前进波和反射波形成驻波，==且在驻点时：幅度=0，速度=0==

在量子力学中，电子运动可以看作波包的运动，波包群速度就是电子运动的平均速度，设波包频率为$\gamma$，电子运动的平均速度可以由：
$$
v = \frac{d\gamma}{dk} \leftarrow
\left{
\begin{aligned}
P &= h \cdot k \
E &= h \gamma
\end{aligned}
\right.
$$

可以解得：

$$
v = \frac{d \frac{E}{h}}{dk} = \frac{1}{h} \cdot \frac{dE}{dk}
$$

又因为在驻点$v=0$
$$
\frac 1h \cdot \frac {dE}{dk}=0
$$
其中的$\frac {dE}{dk}$为方程$E=\frac {h^2k^2}{2m_0}$的斜率

2能带结构

1. 允带禁带：由准自由电子近似可以看出，原先自由电子连续的EK关系被分割为一系列能量允许和不允许的区间，分别称之为允带和禁带
2. 紧束缚近似：从孤立原子核外电子状态出发，把晶体看作是组成晶体的原子相互靠近到一定程度的结果
3. 能级分裂：由于原子的靠近，会使电子的能级发生分裂，其能量有可能处于能级1或者能级2上
   更进一步，电子具有一定几率具有该能级所代表的能量


4. 随着原子互相靠拢，形成晶体，原先孤立原子的电子能级展开形成能带


3布里渊区

当$k=\frac n{za}$时能量出现不连续，形成了一系列相同的允带和禁带，其中：

$－\frac 1{2a}＜k＜\frac 1{2a}$	第Ⅰ布里渊区	简约布里渊区，也称为简约波矢
$－\frac 1{a}＜k＜\frac 1{a}$	第Ⅱ布里渊区


1. 禁带出现在布里渊区边界上，每个布里渊区对应一个能带

2. 由于图中可以看出来，布里渊区具有周期性，其对应的能带对应的有
   $$
   E(k)=E(k+ \frac na），周期为\frac na
   $$

4能带量子化

由于$E=\frac {h^2k^2}{2m_0}$，有了确定的k就可以确定E，一个k对应一个能级，若我们知道一个允带中有多少个k，就可以知道一个能带中有多少个能级
考虑最简单的情况，在一维晶体中：
$$
L_{长度}=N \cdot a，N为原子数，a为晶格常数
$$

根据循环边界条件：
在$x=0$和$x=L$处波函数由于周期性而相等，有：
$$
\psi(0)=\psi(L)，由布洛赫\psi_k(x)=u_k(x) \cdot e^{i2 \pi kx}
$$
故在$x=0$处和$x=L$处
$$
\psi_k(0) = u_k(0) \cdot e^{i2 \pi k 0} = \psi_k(L) = u_k(L) \cdot e^{i2 \pi k L}
$$
由于布洛赫定律的幅值函数也具有周期性，$e^0=1$，有：
$$
\psi_k(0) =1 \cdot 1 = \psi_k(L) = 1\cdot e^{i2 \pi k L}=1
$$
整理得$e^{i2 \pi k L}=1$运用欧拉公式得：
$$
e^{i2 \pi k L}=cos(2 \pi kL)+isin(2 \pi kL)=1
$$
故解得：
$$
2 \pi kL=2 \pi n，n为整数
$$
两边同除：
$$
k=\frac nL=\frac n {Na}
$$
观察公式k离散，得到==能级离散==

5布里渊区和k的关系

一个布里渊区对应一个允带，其中k的个数有如下关系：

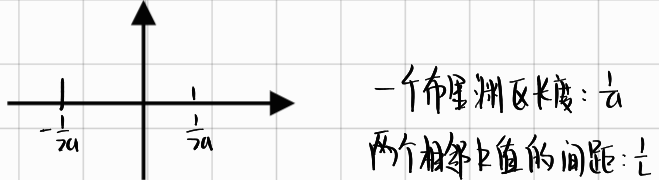
$$
k = \frac {布里渊区宽度}{单位晶格长度} = \frac {\frac 1a}{\frac 1L} = \frac La = \frac {Na}a = N
$$
其中：

• $N$为原子个数，对应$N$个能级
• 一个$k$对应一个能级

6结论

1. 根据泡利不相容原理，每个能级上不可能有两个或两个以上完全相同的电子，但是可以有两个自旋相反的电子处在一个能级；==一个布里渊区可以容纳$2N$个电子==（因为每个布里渊区对应$N$个能级，每个能级上可对应两个自旋相反的电子）

2. 允带中有$N$个分立的能级，其宽度又特别小只有几个$eV$，故其能级分布非常密，甚至可以称之为==准连续==

1.1.4导体半导体和绝缘体的能带

固体物理认为晶体中的电子能够参与导电是因为在外力或者外场作用下，电子的能量状态，以及其在布里渊区的分布情况发生了改变

1在外电场作用条件下满带中电子分布情况

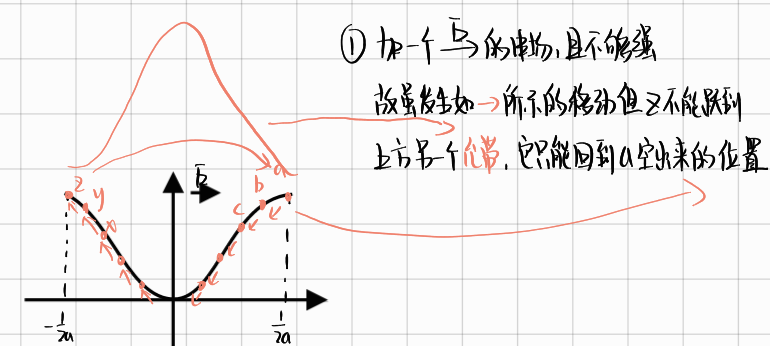
• 在宏观上分布情况并未改变，故==满带中电子不参与导电==
• $k$随$t$均匀变化，由：

$$
dE=|\vec F|dS=-q|\vec E|dS=-q|\vec E|Vdt
$$

​ 又$v=\frac 1h \frac {dE}{dk}dt$带入上式：
$$
dE=-q|\vec E| \cdot \frac 1h\frac {dE}{dk}dt
$$
​ 两边约去$dE$得：
$$
\frac {dk}{dt}=-q|\vec E| \cdot \frac 1h
$$
​ 等式左边都是常数，得$k$随$t$均匀变化

2在外电场作用条件下半满带中电子分布情况

3导体、绝缘体、半导体的能带

4在实验中各元素的禁带宽度

在室温$T=300k$时

元素种类	$Eg$
$Si$	$1.12eV$
$Ge$	$0.67eV$
$GrAs$	$1.43eV$
绝缘体或金刚石	$6 - 7eV$

5本征半导体

• 本征半导体：纯净的，不含任何杂质和缺陷的半导体
• 本征激发：本征半导体中价带电子在电场作用下跃迁到导带的过程，==即共价键上电子挣脱束缚成为自由电子的过程==

1.2半导体中电子的运动

1.2.1半导体中电子的EK关系

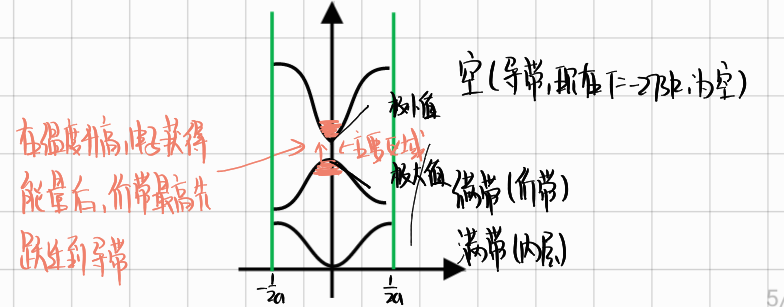
在上图中我们研究的主要区域是$\frac {dE}{dk}=0$

1导带底附近的EK关系（引入了有效质量$m_n^*$）

对于极值$\frac {dE}{dk}=0$在$x_0$附近使用泰勒展开：
$$
f(x)=f(x_0)+f’(x_0)+f’(x_0)(x-X_0)’+\frac 1{2!}f’(x_0)(x-x_0)^2…
$$
在波矢k空间中$x=k=0$：
$$
E(k)=E(k=0)+\frac {dE}{dk}|{k=0}\cdot(k-0)’+\frac 12 \frac{d^2E}{dk^2}(k-0)^2…
$$
将第三项提出：
$$
E(k)-E(0)=\frac 12 \frac{d^2E}{dk^2}k^2 \rightarrow式1
$$
又因为在自由电子中
$$
E(k)-E(0)=\frac {h^2k^2}{2m{0}}\rightarrow式2
$$
将这个式子中的$m_0$换成有效质量$m_{n}^*$，并将式1和式2联立：
$$
\begin{align}
\frac 12 \frac{d^2E}{dk^2}k^2&=\frac {h^2k^2}{2m_{0}}
$$